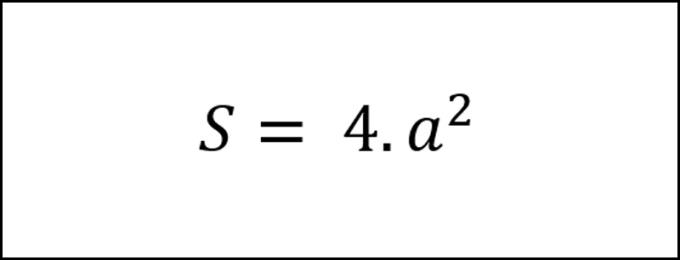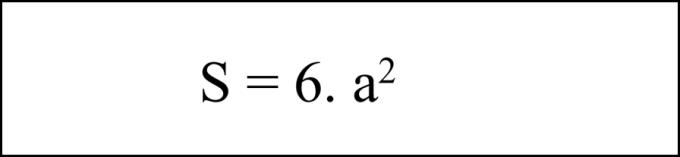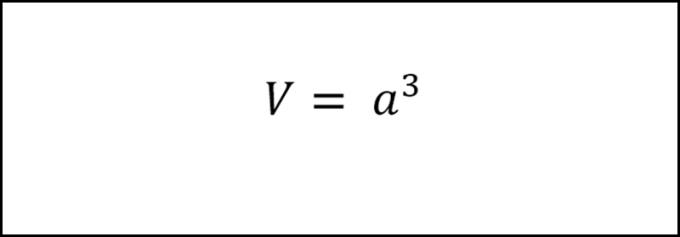De kubus is een van de 3D-geometrieën die in het dagelijks leven veel voorkomen. Hieronder volgen de concepten, eigenschappen en formules voor de oppervlakte van een kubus, evenals het volume ervan. Bovendien levert het ook uiterst nuttige berekeningen op bij het berekenen.
1. Concepten en eigenschappen kubussen
- Concept
Een kubus is een puzzel met 6 vlakken, 8 hoekpunten, 12 randen, alle vlakken zijn gelijke vierkanten, gelijke zijden. Een kubus kan worden opgevat als een kubus met gelijke breedte, lengte en hoogte.
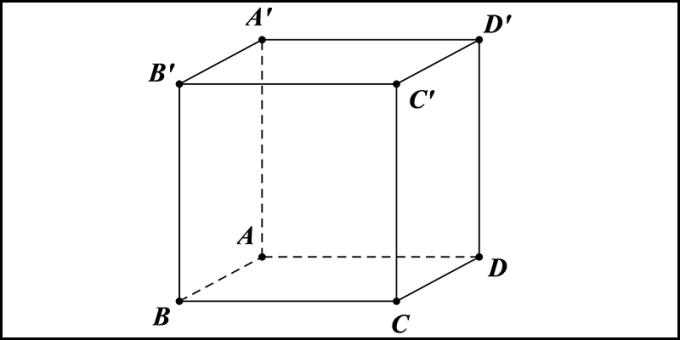
- Eigenschappen van de kubus
+ Er zijn 6 symmetrische en gelijke vlakken.
+ Er zijn 12 gelijke randen.
+ De diagonaal van de zijkanten is gelijk.
+ Diagonale kubussen zijn gelijk.
2. Formule om de oppervlakte van een kubus te berekenen
- Formule om het gebied rond de kubus te berekenen
Het gebied rond de kubus is gelijk aan het kwadraat van de lengtes van één zijde vermenigvuldigd met vier.
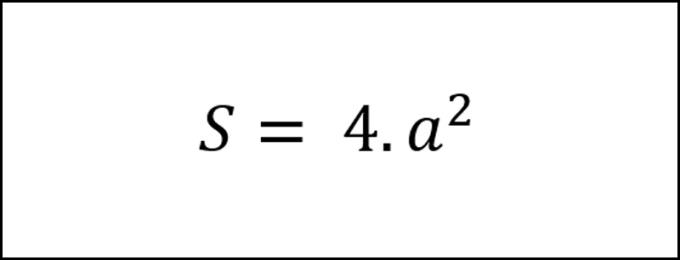
Waarin :
+ a: is de lengte van één zijde.
+ S: is de omgeving.
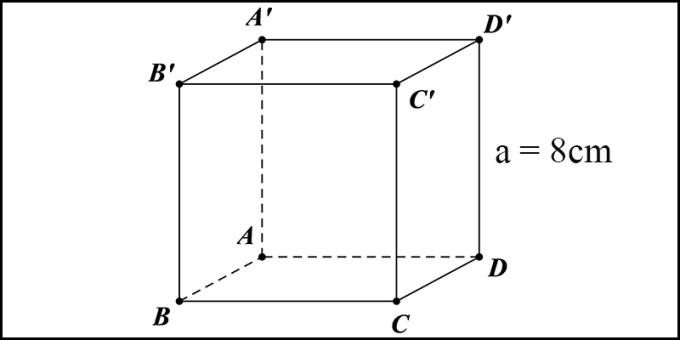
Hier zal WebTech360 u een illustratief voorbeeld sturen om het u gemakkelijker te maken de formule toe te passen. Laat de kubus van A'B'C'D'.ABCD een zijdelengte van 8 cm hebben. Bereken de omgeving.
Formule toepassen. We hebben: S = 4 xaxa = 4 x 8 x 8 = 256 (cm2).
- Formule om de totale oppervlakte van de kubus te berekenen
De totale oppervlakte van de kubus is gelijk aan het kwadraat van de lengtes van één zijde vermenigvuldigd met zes.
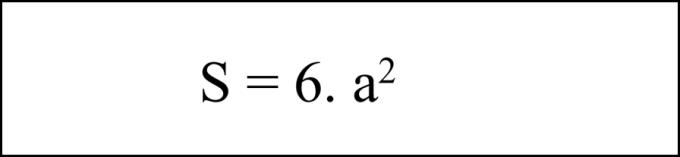
Waarin :
+ a: is de lengte van één zijde.
+ S: is de totale oppervlakte.

Voorbeeld: Gegeven een blauwe kubus die aan één kant 10 cm is. Bereken de totale oppervlakte van de bovenstaande afbeelding.
Als we de bovenstaande formule toepassen, hebben we S = 6 x 10 x 10 = 600 (cm2).
3. Formule voor het berekenen van het volume van een kubus
Het volume van een kubus is gelijk aan een kubus van één zijde.
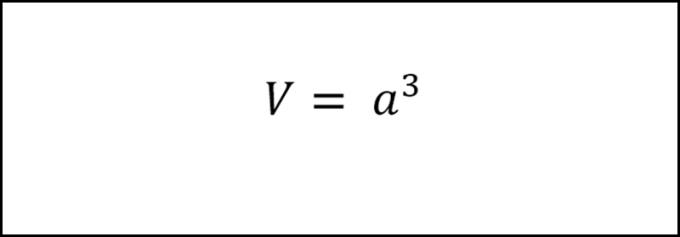
Waarin :
+ a: is de lengte van één zijde.
+ V: is het volume.
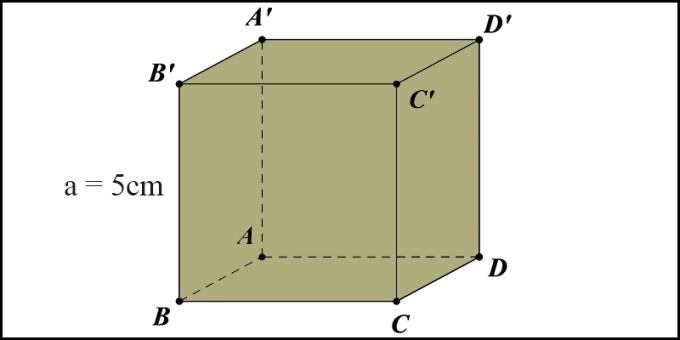
Referentievoorbeeld voor volumeberekening. Laat A'B'C'D'.ABCD-kubus met lengte BB '= 5 cm. Bereken het volume van de kubus.
Als we de formule toepassen, hebben we V = axaxa = 5 x 5 x 5 = 125 (cm3).
4. Let op bij het doen van kubusoefeningen
- Eenheden van volume berekend per blok (bijv. Kubieke meter (m3)).
- Eenheidsoppervlakte berekend in meeteenheden exponentieel 2 (zoals vierkante meter (m2)).
Hopelijk brengt het artikel nuttige kennis. Succes!