Een trapezium is een convexe vierhoek met twee tegenover elkaar liggende evenwijdige zijden. Deze zijden worden de twee basissen van het trapezium genoemd. De overige twee zijden zijn de twee zijkanten.
De hoogte van een trapezium is de afstand van het loodrechte hoekpunt tot de grootste basis. Bij een rechte trapezium is de hoogte van het trapezium gelijk aan één zijde van het trapezium.
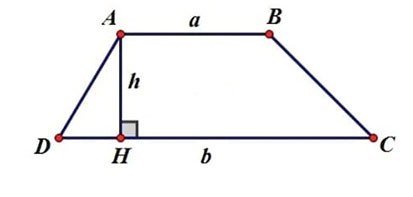
Naast de formule voor het berekenen van de oppervlakte van een trapezium en de formule voor het berekenen van de omtrek van een trapezium , is de formule voor het berekenen van de hoogte van een trapezium ook erg belangrijk en nauw verwant aan vlakke meetkundeproblemen. Het onderstaande artikel helpt u de formule te begrijpen voor het berekenen van de hoogte van een regelmatige trapezium, een gelijkbenige trapezium en een rechte trapezium.
Formule voor het berekenen van de trapeziumhoogte
De formule voor het berekenen van de hoogte van een trapezium is de oppervlakte van de twee bases vermenigvuldigd met 2, gedeeld door de totale lengte van de twee bases.
Voorbeeld van het berekenen van de hoogte van een trapezium
Voorbeeld 1 : De oppervlakte van een trapezium is gelijk aan de oppervlakte van een vierkant met een zijde van 30 cm, de totale lengte van de grootste en de kleinste basis is 75 cm. Hoe hoog is het trapezium?
Prijs:
De oppervlakte van een trapezium is gelijk aan de oppervlakte van een vierkant met een zijde van 30 cm, dus de oppervlakte van het trapezium zal zijn: 30 x 30 = 900 cm2
Trapeziumhoogte is: 900 x 2 : 75 = 24 cm
Voorbeeld 2 : Een trapezium heeft een kleine basis die 60% van de grote basis bedraagt, 24 cm minder dan de grote basis. Vraag hoe hoog de trapezium is, wetende dat de oppervlakte van het trapezium 720 cm2 is.
Prijs:
De kleine basis is: 24 : (5 - 3) x 3 = 36 cm
Grote basis: 24 + 36 = 60
Trapeziumvormige hoogte:
Studenten hebben een specifiek type laptop nodig voor hun studie. Deze moet niet alleen krachtig genoeg zijn om goed te presteren in hun studierichting, maar ook compact en licht genoeg om de hele dag mee te nemen.
Het toevoegen van een printer aan Windows 10 is eenvoudig, hoewel het proces voor bekabelde apparaten anders is dan voor draadloze apparaten.
Zoals u weet, is RAM een zeer belangrijk hardwareonderdeel van een computer. Het fungeert als geheugen voor de verwerking van gegevens en is de factor die de snelheid van een laptop of pc bepaalt. In het onderstaande artikel laat WebTech360 u zien hoe u met behulp van software in Windows RAM-fouten kunt opsporen.
Smart-tv's hebben de wereld veroverd. Dankzij zoveel geweldige functies en internetverbinding heeft technologie de manier waarop we televisiekijken veranderd.
Koelkasten zijn vertrouwde apparaten in huishoudens. Koelkasten hebben meestal twee compartimenten. Het koelvak is ruim en heeft verlichting die automatisch aangaat wanneer de gebruiker het vak opent. Het vriesvak is smal en heeft geen verlichting.
Wi-Fi-netwerken worden niet alleen beïnvloed door routers, bandbreedte en interferentie, maar er zijn een aantal slimme manieren om uw netwerk te versterken.
Als u terug wilt naar de stabiele iOS 16 op uw telefoon, vindt u hier de basisgids voor het verwijderen van iOS 17 en downgraden van iOS 17 naar 16.
Yoghurt is een heerlijk voedingsmiddel. Is het goed om elke dag yoghurt te eten? Hoe verandert je lichaam als je elke dag yoghurt eet? Laten we het samen ontdekken!
In dit artikel worden de meest voedzame rijstsoorten besproken en hoe u de gezondheidsvoordelen van de rijst die u kiest, optimaal kunt benutten.
Een slaapschema en bedtijdroutine opstellen, uw wekker verzetten en uw dieet aanpassen zijn enkele maatregelen die u kunnen helpen om beter te slapen en 's ochtends op tijd wakker te worden.
Huren alstublieft! Landlord Sim is een simulatiespel voor mobiel op iOS en Android. Je speelt als verhuurder van een appartementencomplex en begint met het verhuren van een appartement. Je doel is om het interieur van je appartement te verbeteren en het gereed te maken voor huurders.
Ontvang de Roblox-gamecode voor Bathroom Tower Defense en wissel deze in voor geweldige beloningen. Ze helpen je bij het upgraden of ontgrendelen van torens met hogere schade.
Laten we op de meest nauwkeurige manier de structuur, symbolen en werkingsprincipes van transformatoren leren kennen.
Van betere beeld- en geluidskwaliteit tot spraakbesturing en meer: deze AI-functies maken smart-tv's zoveel beter!
Aanvankelijk hadden mensen hoge verwachtingen van DeepSeek. Deze AI-chatbot wordt op de markt gebracht als sterke concurrent van ChatGPT en belooft intelligente chatmogelijkheden en -ervaringen.
