In het onderstaande artikel zal Quantrimang.com gedetailleerd wat inhoud delen met lezers over het onderwerp formules voor het berekenen van het volume van een kegel, het laterale oppervlak en het totale oppervlak van een kegel. Raadpleeg deze informatie.
Inhoudsopgave
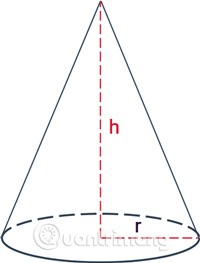
Een piramide ontstaat door een rechthoekige driehoek één omwenteling om zijn as (een rechthoekige zijde) te draaien.
Bereken de oppervlakte van de kegel
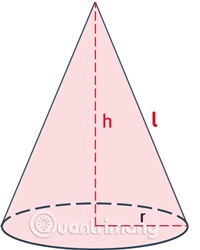
Het oppervlak van een kegel wordt vaak in twee termen aangeduid: omringend en totaal.
- Het laterale oppervlak van een kegel omvat alleen het oppervlak rondom de kegel, niet het oppervlak van de basis.
- Het totale oppervlak wordt berekend als de grootte van de gehele ruimte die door de figuur wordt ingenomen, inclusief het laterale oppervlak en het oppervlak van de cirkelvormige basis.
Concreet als volgt:
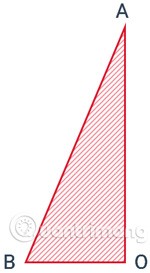
Gegeven een rechthoekige driehoek ABO in O, zal draaien om de vaste rechte zijde OA een kegel opleveren.
- De rand OB loopt door tot de basis van de kegel, die een cirkel is met het middelpunt O.
- Rand AB veegt over het omliggende oppervlak van de kegel, elk van zijn posities wordt een generator genoemd, bijvoorbeeld AB is een generator.
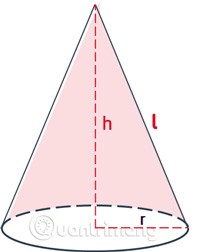
- A is de top en AO is de hoogte van de kegel.
|
 |
|
Formule voor het berekenen van de laterale oppervlakte: gelijk aan de helft van het product van de omtrek van de basiscirkel en de lengte van de genererende lijn.
 |
Toegepast op het specifieke voorbeeld hierboven:
Daarin:
- De omtrek is het gebied rondom de kegel.
ris de straal van de basis van de kegel.lis de lengte van de generatorlijn van de kegel.
|
Formule voor het berekenen van de totale oppervlakte: is gelijk aan de laterale oppervlakte plus de basisoppervlakte.
Bereken het volume van een kegel
Het volume van een kegel is de hoeveelheid ruimte die de kegel inneemt.
Formule voor het berekenen van het volume van een kegel: gelijk aan 1/3 van het basisoppervlak vermenigvuldigd met de hoogte
Daarin:
Vis het volume van de kegel.ris de basisstraal van de kegel.his de hoogte, de afstand tussen de bovenkant en de basis van de kegel.
Bepaal de generator, hoogte en basisstraal
De hoogte is de afstand van het middelpunt van de basis tot de top van de piramide.
De generator is de afstand van elk punt op de basiscirkel tot de top van de piramide.
Omdat een kegel ontstaat wanneer een rechthoekige driehoek één keer rond de as van een van zijn rechthoekige zijden wordt gedraaid, kunnen de hoogte en de straal van de basis worden beschouwd als de twee rechthoekige zijden van de driehoek, en de generator is de hypotenusa.
Als we de hoogte en de basisstraal kennen, kunnen we de genererende lijn berekenen met behulp van de formule:
Als u de hoogte en de generator kent, berekent u de basisstraal volgens de formule:
Hierboven staan de formules voor het berekenen van de laterale oppervlakte, de totale oppervlakte en het volume van een kegel. Bedankt dat u het artikel volgt.