Formule voor het berekenen van de diagonaal van een ruit

Een ruit is een vierhoek met vier gelijke zijden, een vierhoek met twee diagonalen die loodrecht op elkaar staan ​​in het midden van elke lijn is een ruit, een parallellogram met twee aaneengesloten zijden die gelijk zijn... Naast vierkanten, rechthoeken, driehoeken... is de ruit een van de belangrijkste vormen in de wiskunde en het leven.

Naast de formule om de omtrek en de oppervlakte van een ruit te berekenen , is de manier om de diagonaal van een ruit te berekenen - de lijn die de tegenoverliggende hoekpunten van de ruit met elkaar verbindt - ook erg belangrijk.

Het onderstaande artikel helpt u bij het berekenen van de diagonaal van een ruit, aan de hand van specifieke voorbeelden. Raadpleeg hiervoor het artikel.

Inhoudsopgave

• Diagonaal van een ruit
• Eigenschappen van de diagonalen van een ruit
• Formule voor het berekenen van de diagonaal van een ruit
• Probleem bij het berekenen van de diagonaal van de ruit

Diagonaal van een ruit

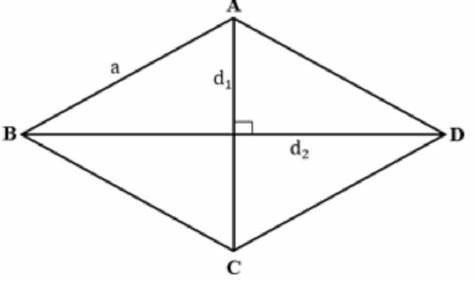
• De diagonaal van een ruit is de lijn die twee tegenover elkaar liggende hoekpunten van de ruit verbindt.
• Een ruit bestaat uit twee diagonalen. Deze snijden elkaar in het midden van de ruit.
• De diagonaal verdeelt de ruit in twee gelijkzijdige driehoeken met gelijke zijden.

Eigenschappen van de diagonalen van een ruit

De twee diagonalen van een ruit hebben de volgende eigenschappen:

• Twee gelijke diagonalen: De twee diagonalen van een ruit zijn even lang.
• De hoek tussen twee diagonalen is een rechte hoek: De twee diagonalen van een ruit snijden elkaar in het midden van de ruit en vormen een rechte hoek.
• Diagonalen zijn de symmetrieassen van een ruit. Elke diagonaal van een ruit is een symmetrieas van de ruit en verdeelt de ruit in twee symmetrische helften.
• Diagonalen zijn de diagonalen van twee gelijkzijdige driehoeken. Elke diagonaal van een ruit is een diagonaal van twee gelijkzijdige driehoeken, gevormd door gelijke zijden.
• Het product van de lengtes van de twee diagonalen is gelijk aan het product van de lengtes van de twee zijden van een ruit. Dat wil zeggen, als we de diagonaal aanduiden met d, en de zijden met a en b, dan geldt d² = a² + b².

Deze eigenschappen zijn karakteristieke eigenschappen van ruiten en worden gebruikt in veel geometrische problemen met ruiten.

Formule voor het berekenen van de diagonaal van een ruit

Bekijk het onderstaande voorbeeld om de formule voor het berekenen van de diagonaal van een ruit af te leiden.

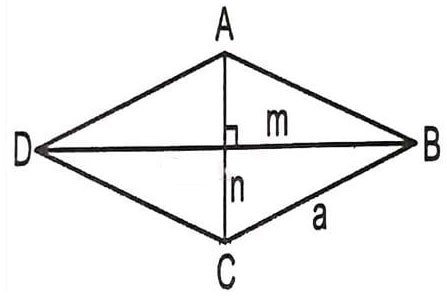
Stel dat we de lengte van de diagonaal van een ruit ABCD met zijde a en hoek ABC = 60 graden moeten berekenen -> wat is de formule om in dit geval de diagonaal van een ruit te berekenen?

Oplossing:

Omdat ABCD een ruit is, zijn alle zijden gelijk aan a.

Beschouw driehoek ABC met: AB = BC = a

Nogmaals: ABC = 60 graden => Driehoek ABC is een gelijkzijdige driehoek met zijde a.

=> AB = AC = BC = a

=> De lengte van de diagonaal van de ruit is AC = BD = a.

De bovenstaande oplossing is een van de eenvoudigste en gemakkelijkst te begrijpen formules voor het berekenen van de diagonaal van een ruit.

Formule voor het berekenen van de diagonaal van een ruit als de oppervlakte en de resterende diagonaal bekend zijn

Uit de formule voor het berekenen van de oppervlakte van een ruit:

S = (axb) : 2

De formule voor de diagonale lengte is als volgt:

a = S x 2 : b

of

b = S x 2 : a

Daarin:

• S is het gebied
• a en b zijn de lengtes van de twee diagonalen

Gebruik de geometrische eigenschappen van een ruit om de lengte van de diagonaal te berekenen zonder de stelling van Pythagoras te gebruiken. Meer specifiek:

De diagonaal van een ruit is het gemiddelde van de twee hoogten.

Diagonaal = vierkantswortel van (lange hoogte + korte hoogte)²

De diagonaal van een ruit is de helft van de omtrek van de ruit.

Diagonaal = 1/2 x omtrek van de ruit.

Probleem bij het berekenen van de diagonaal van de ruit

Probleem 1: Gegeven een ruit met een oppervlakte van 360 vierkante centimeter en een diagonaal van 24 centimeter. Bereken de lengte van de tweede diagonaal

Oplossing:

Volgens de formule voor de oppervlakte van een ruit: axb : 2

We hebben de tweede diagonaal: 360 x 2 : 24 = 30 cm

Antwoord: 30 cm

Probleem 2:

Een ruit heeft een oppervlakte van 4 dm, de lengte van één diagonaal is 3/5 dm. Bereken de lengte van de tweede diagonaal. Oplossing:

De lengte van de tweede diagonaal is:

(4 x 2) : 3/5 = 40/3 (dm)

Les 3: De twee diagonalen van een ruit zijn 160 cm en 120 cm lang. Bereken de hoogte van de ruit. De verhouding tussen de hoogte en de lengte van de zijde van de ruit is 24:25.

Oplossing:

De oppervlakte van de ruit is: 160,120:2 = 9600 (cm2).

Omdat de verhouding tussen de hoogte en de lengte van de zijde van een ruit 24:25 is, kunnen we de hoogte van de ruit als 24a beschouwen en de zijde van de ruit als 25a.

Dan hebben we de oppervlakte van de ruit: 25a.24a = 9600 a2 = 16 a = 4 cm.

De hoogte van de ruit is: 24,4 = 96 (cm).

De hoogte van de ruit is dus 96 cm.

Les 4: 

Gegeven ruit ABCD met zijlengte 12,5 cm, hoogte 6,72 cm en AC is kleiner dan BD. Wat zijn de lengtes van de diagonalen AC en BD?

Prijs:

Pas de formule toe om de oppervlakte van een ruit te berekenen: S = ha = 6,72 x 12,5 = 84 cm.
=> 1/2 AC x BD = 84 => 2AC.BD = 336

Laat O het snijpunt zijn van de twee diagonalen van een ruit.

We hebben AOB is een rechthoekige driehoek in O, dus AB2 = OA2 + OB2

Waarin OA = 1/2 AC, OB = 1/2 BD

=> 12,52 = 1/4 (AC2 + BD2) <=> 625 = AC2 + BD2

AC2 + BD2 = 625 <=> AC2 + BD2 + 2AC.BD = 625 + 336 <=> (AC + BD)2 = 961 <=> AC + BD = 31 (1)

AC2 + BD2 = 625 <=> AC2 + BD2- AC.BD = 625 -336 <=> (BD - AC)2 = 289 <=> BD - AC = 17 (Volgens het probleem BD > AC) (2)

Uit (1) en (2) hebben we:

BD = 24, AC = 7 cm.

Les 5: 

Ruit ABCD heeft zijden gelijk aan 10 eenheden. Bereken de lengte van de diagonaal van de ruit.

Oplossing: De lengte van de diagonaal van ruit ABCD is:

Diagonaal = vierkantswortel van 2(10²) = vierkantswortel van 200 = 14,14 lengte-eenheden.

De lengte van de diagonaal van ruit ABCD bedraagt ​​dus 14,14 lengte-eenheden.

Les 6:

Ruit ABCD heeft een diagonaal van 12 eenheden. Bereken de omtrek van de ruit.

Oplossing: Omdat een ruit vier gelijke zijden heeft, zal de omtrek de som zijn van de lengtes van de vier zijden, dat wil zeggen:

Omtrek = 4 x zijdelengte = 4 x 6 = 24 lengte-eenheden.

De omtrek van ruit ABCD is dus 24 lengte-eenheden.