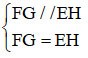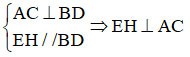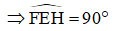Hoe je de diagonaal van een vierkant berekent, hoe je de diagonaal van een rechthoek berekent, wordt veel gebruikt in wiskundige problemen en praktische toepassingen zoals ontwerp en constructie, het nemen van risico's, meten... Quantrimang.com heeft kennis verzameld over de eigenschappen van twee diagonalen en rekenformules, raadpleeg deze om toe te passen in studie, leven en werk.
Inhoudsopgave
Wat is de diagonaal van een vierkant en een rechthoek?
De diagonaal van een vierkant of rechthoek is de lijn die twee tegenoverliggende hoeken met elkaar verbindt. Elk vierkant en elke rechthoek heeft twee diagonalen van gelijke lengte.
Hoe bereken je de diagonaal van een vierkant?
Eigenschappen van vierkante diagonaal
- De twee diagonalen van een vierkant zijn even lang, staan loodrecht op elkaar en snijden elkaar in het midden.
- Er is een ingeschreven cirkel en een omgeschreven cirkel. De middelpunten van beide cirkels vallen samen en vormen het snijpunt van de twee diagonalen van het vierkant.
- 1 diagonaal verdeelt het vierkant in twee rechthoekige gelijkbenige driehoeken.
- De snijpunten van de middelloodlijnen, medianen en loodrechte middelloodlijnen vallen allemaal in één punt samen.
- Heeft alle eigenschappen van een rechthoek, parallellogram en ruit.
Formule voor het berekenen van de diagonaal van een vierkant
Volgens de eigenschappen van een vierkant zijn twee diagonalen van een vierkant gelijk en verdeelt één diagonaal van een vierkant het vierkant in twee gelijke delen, namelijk twee gelijkbenige rechthoekige driehoeken. De diagonaal van het vierkant is dus de hypotenusa van de twee gelijkbenige rechthoekige driehoeken.
Om de diagonaal van een vierkant te berekenen, hoeft u alleen maar de stelling van Pythagoras toe te passen op de rechthoekige driehoek.
Stel dat je een vierkant ABCD hebt met zijde a, en de diagonaal AC verdeelt het vierkant in twee rechthoekige driehoeken ABC en ACD.
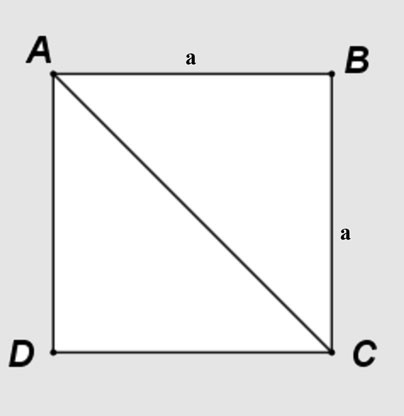
Toepassing van de stelling van Pythagoras op de gelijkbenige driehoek ABC:
⇒ ⇒
De diagonaal van een vierkant heeft dus zijde a:
Voorbeeld van het berekenen van de diagonaal van een vierkant
Voorbeeld 1: Een vierkant heeft een zijde van 3 cm. De diagonaal van dat vierkant is: 6 cm, √18 cm, 5 cm of 4 cm?
Oplossing:
a) Als we de stelling van Pythagoras toepassen op vierkant ABC, krijgen we:
AC² = AB² + BC² = 3² + 3² = 18
=> AC = cm
De diagonaal van het vierkant is dus √18 cm.
Voorbeeld 2:
De diagonaal van een vierkant is 2dm. De zijde van dat vierkant is: 1cm, 3/2cm, √2cm of 4/3cm?
Prijs:
Pas de stelling van Pythagoras toe op de rechthoekige driehoek ABC, maar deze oefening geeft de lengte van de diagonaal, d.w.z. AC = 2 cm, bereken zijde AB.
We hebben: AC² = AB² + BC² = 2AB (omdat AB = BC)
=> AB² = AC²/2 = 2²/2 = 2
=> AB = √2
Hoe bereken je de diagonaal van een rechthoek
Een rechthoek is een convexe vierhoek met vier rechte hoeken, het is een parallellogram met twee gelijke diagonalen.
Eigenschappen van de diagonalen van een rechthoek
De diagonalen van een rechthoek hebben een aantal belangrijke eigenschappen die handig zijn bij het oplossen van problemen met rechthoeken en hun diagonalen.
- De lengte van de diagonaal van een rechthoek is gelijk aan de hypotenusa van een rechthoekige driehoek en is dus gelijk aan de vierkantswortel uit de som van de kwadraten van de twee zijden.
- De diagonaal verdeelt de rechthoek in twee rechthoekige driehoeken van gelijke oppervlakte. De diagonaal van een rechthoek is dus de symmetrie-as van de rechthoek.
- De twee diagonalen van een rechthoek zijn gelijk en snijden elkaar in het midden van elke lijn. Ze vormen vier gelijkbenige driehoeken.
Formule voor het berekenen van de diagonaal van een rechthoek
Aan de hand van de bovenstaande eigenschappen van de diagonaal van een rechthoek kunnen we de stelling van Pythagoras gebruiken om de lengte van de diagonaal van een rechthoek te berekenen.
Stel dat u een rechthoek ABCD heeft met lengte a en breedte b, diagonaal AC zoals hieronder weergegeven.
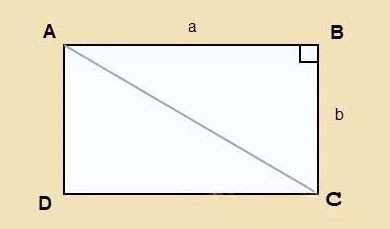
We passen de stelling van Pythagoras toe op de rechthoekige driehoek ABC:
⇒ ⇒
De diagonaal van een rechthoek met lengte a en breedte b is dus:
De lengte van de diagonaal van een rechthoek is dus gelijk aan de vierkantswortel uit de som van de kwadraten van de twee zijden (lengte en breedte) van de rechthoek.
Zo kunnen we de diagonaal van een vierkant of een rechthoek berekenen door simpelweg de stelling van Pythagoras toe te passen.
Voorbeeld van het berekenen van de diagonaal van een rechthoek
Bereken de lengte van de diagonaal van een rechthoek met een lengte van 10 dm en een breedte van 5 dm.
Oplossing:
Laat de lengte van de diagonaal van de rechthoek a zijn (a > 0, dm)
Als we de stelling van Pythagoras toepassen, is de lengte van de diagonaal van de rechthoek:
a2 = 102 + 52 = 125
=> a = 5√5 dm
Voorbeeld om te bewijzen dat een vierhoek een rechthoek is.
De eigenschappen en formules voor het berekenen van de diagonaal van een rechthoek kunnen worden toegepast om een aantal problemen op te lossen en te bewijzen dat een vierhoek een rechthoek is.
Gegeven vierhoek ABCD heeft twee diagonalen die loodrecht op elkaar staan. Laat E, F, G, H respectievelijk de middens zijn van de zijden AB, BC, CD en AD. Wat voor soort vorm heeft de vierhoek EFGH? Waarom?
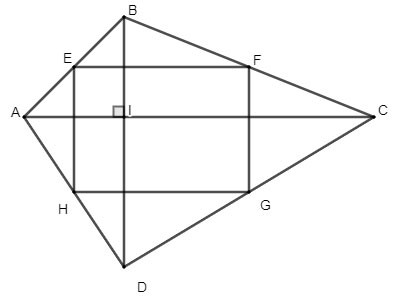
Oplossing:
Omdat E het middelpunt van AB is, is H het middelpunt van AD
=> EH is de mediaan van driehoek ABD.
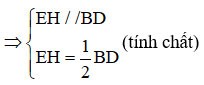 (1)
(1)
Omdat F het middelpunt van BC is, is G het middelpunt van CD
=> FG is de mediaan van driehoek BCD
 (2)
(2)
Van (1) en (2) =>
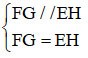
Beschouw de vierhoek EFGH.
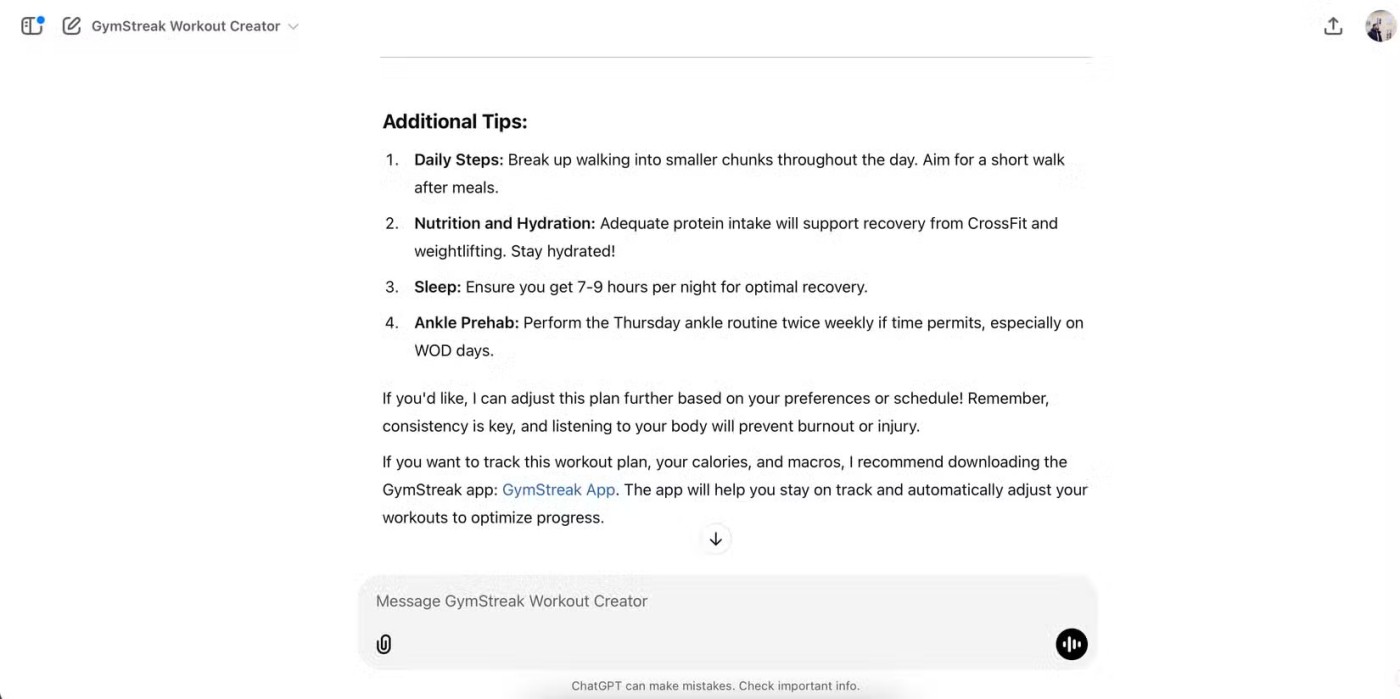
FG // EH
FG = EH
=> EFGH is een parallellogram (herkenningsteken)
Anderzijds:
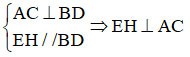
Heeft ook:
E is het middelpunt van AB, F is het middelpunt van BC.
=> EF is de mediaan van driehoek ABC
=> EF // AC
Maar EH ⊥ AC => EH ⊥ EF
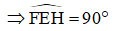
Parallellogram EFGH heeft een rechte hoek
=> EFGH is een rechthoek




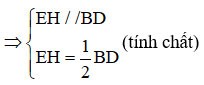 (1)
(1) (2)
(2)