Formule voor het berekenen van de oppervlakte van de ruit, de omtrek van de ruit

Laten we de formule voor het berekenen van de oppervlakte, de omtrek van een ruit en de diagonaal van een ruit uit het onderstaande artikel nog eens doornemen en onthouden.

Inhoudsopgave

• 1. Formule voor het berekenen van de oppervlakte van een ruit
  • Formule voor het berekenen van de oppervlakte van een ruit op basis van de basis en de hoogte
  • Formule voor het berekenen van de oppervlakte van een ruit op basis van de driehoeksformule (als u de hoek van de ruit kent)
• 2. Formule voor het berekenen van de omtrek van een ruit
• 3. Wat is een ruit?
  • Eigenschappen van ruit
• 4. Voorbeeld van het berekenen van de oppervlakte en omtrek van een ruit

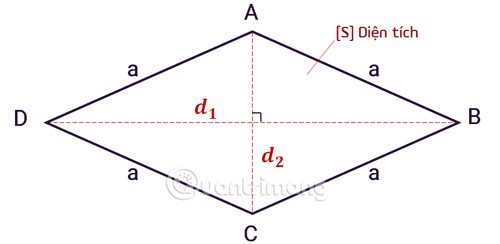
1. Formule voor het berekenen van de oppervlakte van een ruit

De oppervlakte van een ruit wordt gemeten aan de hand van het oppervlak; het zichtbare, platte gedeelte van de ruit.

Formule voor het berekenen van de oppervlakte van een ruit op basis van de basis en de hoogte

De oppervlakte van een ruit is gelijk aan de helft van het product van de lengtes van de twee diagonalen , de formule luidt als volgt:

Daarin:

• Sis de oppervlakte van de ruit.
• d1en d2zijn de twee diagonalen van een ruit.

Voorbeeld van het berekenen van de oppervlakte van een ruit.

Les 1: Er is een ruitvormig stuk karton met twee kruisende diagonalen van respectievelijk 6 cm en 8 cm lang. Wat is de oppervlakte van het ruitvormige karton?

Als we de methode voor het berekenen van de oppervlakte van een ruit toepassen, krijgen we d1 = 6 cm en d2 = 8 cm. We vullen dit in de formule in en krijgen het volgende resultaat:

S = 1/2 x (d1 x d2) = 1/2 (6 x 8) = 1/2 x 48 = 24 cm2

Formule voor het berekenen van de oppervlakte van een ruit op basis van de driehoeksformule (als u de hoek van de ruit kent)

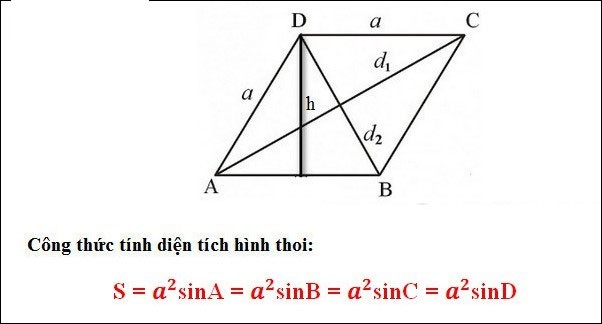
Waarin: a: zijde van ruit

Voorbeeld 1 : Gegeven ruit ABCD, met ruitrand = 4 cm, hoek A = 35 graden. Bereken de oppervlakte van ruit ABCD.

Oplossing: Als we de formule toepassen, krijgen we a = 4, hoek = 35 graden. We vervangen de formule als volgt:

S = a2 x sinA = 42 x sin(35) = 9,176 (cm2)

2. Formule voor het berekenen van de omtrek van een ruit

De omtrek van een ruit wordt berekend door de lengtes van de lijnen rondom de vorm bij elkaar op te tellen. Deze lijnen zijn tevens de lijnen rondom het gehele oppervlak.

Om de omtrek van een ruit te berekenen, berekenen we de som van de lengtes van de vier zijden. De specifieke formule is als volgt:

Daarin:

• Pis de omtrek van de ruit.
• ais de lengte van de zijde van de ruit.

Bijvoorbeeld: Gegeven een ruit ABCD met gelijke zijden en 7 cm. Wat is de omtrek van deze ruit?

Volgens de hierboven gegeven formule voor het berekenen van de omtrek van een ruit, geldt a = 7 cm. De omtrek van ruit ABCD wordt dus als volgt berekend:

P (ABCD) = ax 4 = 7 x 4 = 28 cm

3. Wat is een ruit?

Een ruit is een vierhoek met vier gelijke zijden. Dit is een parallellogram met twee aan elkaar grenzende zijden die gelijk zijn, of een parallellogram met twee diagonalen die loodrecht op elkaar staan.

Eigenschappen van ruit

• 2 gelijke tegenoverliggende hoeken
• 2 diagonalen staan ​​loodrecht op elkaar en snijden elkaar in het midden van elke lijn
• De twee diagonalen zijn de bisectoren van de hoeken.

In dit artikel introduceert Quantrimang.com effectieve formules voor het berekenen van de oppervlakte en omtrek van een ruit voor uw studie en werk.

4. Voorbeeld van het berekenen van de oppervlakte en omtrek van een ruit

Voorbeeld 1: 

Gegeven ruit ABCD met zijde AD = 4 m, hoek DAB = 30 graden. Bereken de oppervlakte van ruit ABCD.

Prijs:

Omdat ABCD een ruit is, zijn de gevormde driehoeken gelijkbenige driehoeken. Laat I het middelpunt zijn van de twee diagonalen, zodat AI loodrecht op BD staat, hoek IAB = 15 graden.

Dus: AI = AB. cos IAB = 4. Cos 15 = 3,84m.

Beschouw de rechthoekige driehoek ABI. Volgens de stelling van Pythagoras geldt:

BI2= AB2- AI2= 1,25m

Dus BI = 1,1m

AC = 2. AI = 7,68 m

BD = 2.BI = 2,2m

Op basis van de formule voor het berekenen van de oppervlakte van een ruit, geldt dat de oppervlakte van de ruit ABCD = ½. Wisselstroom. BD = 8,45(m2)

Voorbeeld 2: Gegeven een ruit met een zijde van 6 cm en een van de hoeken heeft een afmeting van 60°. Bereken de oppervlakte van de ruit.

Met deze gegevens kunt u de oppervlakte van een ruit niet berekenen. Om de diagonaal van een ruit te berekenen, moet je vertrouwen op de eigenschappen van ruiten, eigenschappen van gelijkzijdige driehoeken en op het berekenen van de zijden van een rechthoekige driehoek. De stappen zijn als volgt:

Stap 1: Teken een plaatje en noteer de bekende feiten.

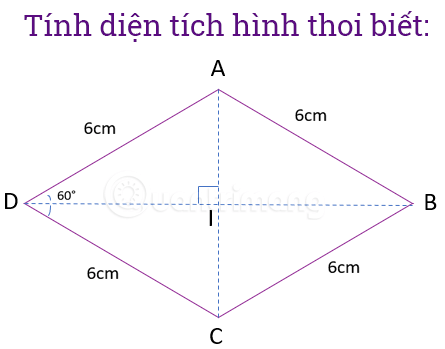
Stap 2: Door de eigenschappen van een ruit toe te passen, hebben we:

, diagonaal AC is de bissectrice van hoek A, dus de hoek zal gelijk zijn aan de helft van de hoek en gelijk zijn aan 60°. (De som van de binnenhoeken van een vierhoek is 360°, de som van de binnenhoeken van een driehoek is 180°). Driehoek ADC is dus een gelijkzijdige driehoek => zijde AC is 6 cm. I is het middelpunt van AC => AI=3cm.

Stap 3: Bereken de lengte van DI

Driehoek DIA is loodrecht op I, zijde DI wordt als volgt berekend:

=> cm

Stap 4: Bereken de oppervlakte van ruit ABCD:

Voorbeeld 3: Gegeven de ruit ABCD met zijde 13 cm, waarbij twee diagonalen elkaar in H snijden.

Bereken de oppervlakte van ruit ABCD, wetende dat BH anderhalf keer zo groot is als AH.

Oplossing:

ABCD is een ruit, dus AH staat loodrecht op BH in H, en driehoek ABH is dan ook rechthoekig in H.

Zij BH = 2a, dan is AH = 3a.

Volgens de stelling van Pythagoras geldt: AH² + BH² = AB² ⇒ 9a² + 4a² = 13 ⇒ 13a² = 13 ⇒ a = 1

Daarom is AH = 3 cm, BH = 2 cm of AC = 6 cm, BD = 4 cm

De oppervlakte van de ruit is: S = 6,4 / 2 = 12 cm².

Voorbeeld 4 :

Gegeven ruit MNPQ, hoek A = 30o, omtrek = 20 m, middelpunt van de diagonaal is I. Wat is de oppervlakte van ruit MNPQ?

Oplossing

De lengte van de zijde van de ruit is a = P : 4 = 20 : 4 = 5m

Omdat de driehoeken die door ruiten worden gecreëerd allemaal gelijkbenige driehoeken zijn, zal de driehoek die wordt gecreëerd vanuit het middelpunt van diagonaal I, punten M, N, worden gecreëerd door hoek IMN = 15o

Lengte van de halve diagonaal MI = MN x cos IMN = 5 x cos150 = 4,8 m

Als we de stelling van Pythagoras toepassen op rechthoekige driehoek MNI, krijgen we: NI = 1,4m

Diagonale lengte NQ = 2 x NI = 2 x 1,4 = 2,8 m

Het oppervlak van de ruit MNPQ is S = 2 x ½ x NQ x MI = 1 x ½ x 2,8 x 4,8 = 13,44 m2

Antwoord: 13,44m2

Als u vragen hebt over de formule voor het berekenen van de oppervlakte en de omtrek van een ruit, laat dan hieronder een reactie achter. We bespreken de vragen graag met u en beantwoorden ze samen. Bedankt dat u het artikel volgt.