Wat is de formule voor het berekenen van de oppervlakte van een regelmatige, rechthoekige en gelijkbenige driehoek ? Raadpleeg het onderstaande artikel om de eenvoudigste en meestgebruikte manieren te begrijpen om de oppervlakte van een driehoek te berekenen.
Inhoudsopgave
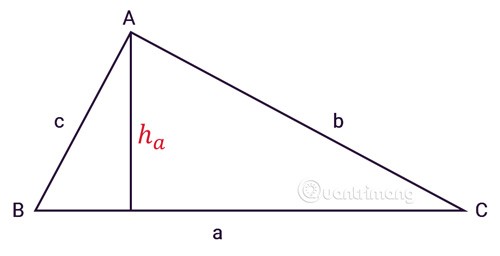
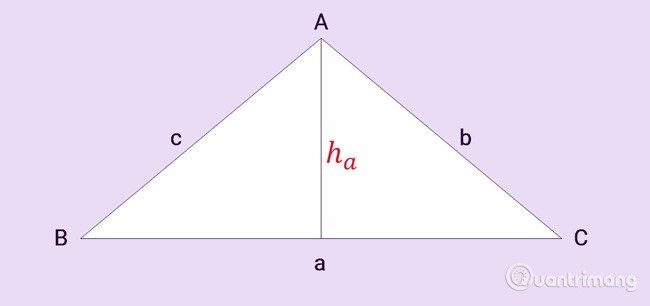
Driehoek ABC heeft drie zijden a, b, c, ha is de hoogte vanaf hoekpunt A zoals weergegeven:
De oppervlakte van een driehoek is gelijk aan de hoogte vermenigvuldigd met de lengte van de tegenoverliggende zijde (de basis) en gedeeld door 2.
Gedicht over het berekenen van de oppervlakte van een regelmatige driehoek
De oppervlakte van een driehoek is eenvoudig.
Vermenigvuldig de hoogte met de basis en deel dit door twee.
Bijvoorbeeld:
Bereken de oppervlakte van een driehoek met een basislengte van 5 m en een hoogte van 24 dm.
Oplossing: Hoogte 24dm = 2,4m
De oppervlakte van de driehoek is:
De oppervlakte van een driehoek is gelijk aan de helft van het product van twee aanliggende zijden maal de sinus van de hoek tussen die twee zijden in de driehoek.
Bijvoorbeeld:
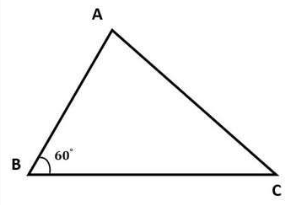
Driehoek ABC heeft zijde BC = 7, zijde AB = 5, hoek B is 60 graden. Oppervlakte van driehoek ABC berekenen?
Prijs:
Met behulp van de bewezen Heron-formule:
Met p de halve omtrek van de driehoek:
Kan worden herschreven met behulp van de formule:
Bijvoorbeeld:
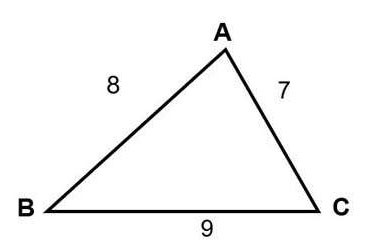
Bereken de oppervlakte van de driehoek met zijdelengtes AB = 8, AC = 7, CB = 9
Prijs:
De halve omtrek van driehoek ABC is
Door de heldenformule toe te passen die we hebben
Ander:
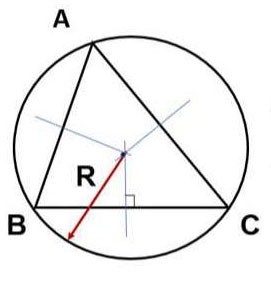
Let op: Het is noodzakelijk om te bewijzen dat R de straal is van de cirkel die de driehoek omschrijft.
Bijvoorbeeld:
Gegeven driehoek ABC, de lengtes van de zijden a = 6, b = 7, c = 5, R = 3 (R is de straal van de cirkel die driehoek ABC omschrijft). Bereken de oppervlakte van driehoek ABC.
Prijs:
Bijvoorbeeld: Bereken de oppervlakte van driehoek ABC als u de lengtes van de zijden kent: AB = 20, AC = 21, BC = 15, r = 5 (r is de straal van de cirkel in driehoek ABC).
Prijs:
De halve omtrek van een driehoek is:
r= 5
De oppervlakte van de driehoek is:
Gelijkbenige driehoeken zijn net als gewone driehoeken. We kunnen de formule toepassen door de hoogte te vermenigvuldigen met de basis en vervolgens te delen door 2, zoals hierboven. Er zullen ook complexere geavanceerde formules zijn:
Gelijkbenige driehoek ABC heeft drie zijden, a is de lengte van de basis, b is de lengte van de twee zijden, ha is de hoogte vanaf hoekpunt A zoals weergegeven:
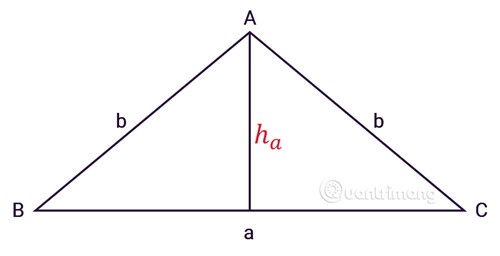
Als we de formule voor het berekenen van de oppervlakte van een regelmatige driehoek toepassen, krijgen we de formule voor het berekenen van de oppervlakte van een gelijkbenige driehoek:
Gelijkzijdige driehoek ABC heeft drie gelijke zijden, a is de lengte van de zijden zoals weergegeven:
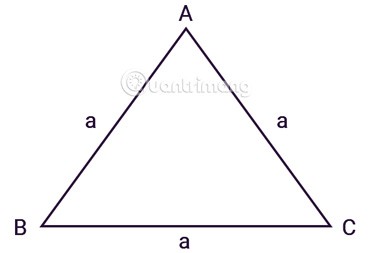
Als we de stelling van Heron toepassen, hebben we de formule voor het berekenen van de oppervlakte van een gelijkzijdige driehoek:
Driehoek ABC is rechthoekig in punt B, a en b zijn de lengtes van de twee rechthoekige zijden:
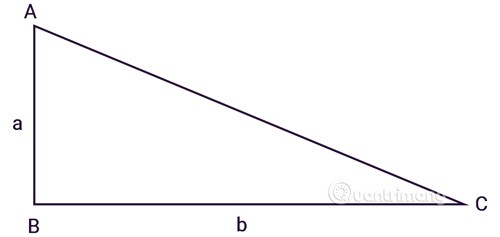
Pas de formule toe voor het berekenen van de oppervlakte van een rechthoekige driehoek, waarbij de hoogte één van de twee rechte zijden is en de basis de resterende zijde.
Formule voor het berekenen van de oppervlakte van een rechthoekige driehoek:
Gedicht over het berekenen van de oppervlakte van een rechthoekige driehoek:
Driehoek met twee rechte hoeken.
Blijf kalm, raak niet in paniek en maak geen fouten.
Zijde, zijde vermenigvuldigd, gedeeld door twee
is de oppervlakte, doe de oefening snel
Driehoek ABC is een rechthoekige driehoek in A, a is de lengte van de twee zijden:
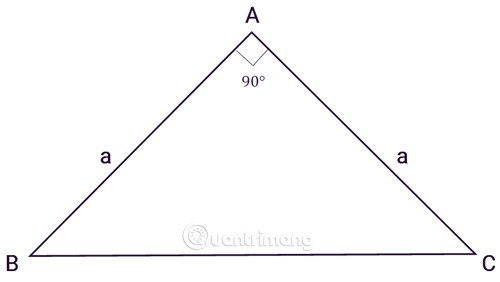
Als we de formule voor het berekenen van de oppervlakte van een rechthoekige driehoek toepassen op de oppervlakte van een gelijkbenige rechthoekige driehoek met gelijke hoogte en basis, krijgen we de formule:
Theoretisch kunnen we de bovenstaande formules gebruiken om de oppervlakte van een driehoek in de ruimte of in de Oxyz-ruimte te berekenen. Dit zal echter wel tot enige rekenproblemen leiden. Daarom berekent men in de Oxyz-ruimte vaak de oppervlakte van een driehoek met behulp van het richtingsproduct.
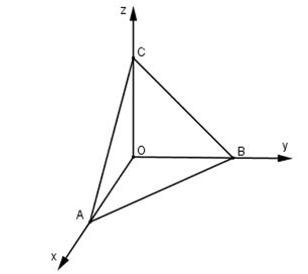
In de ruimte Oxyz, gegeven driehoek ABC. De oppervlakte van driehoek ABC wordt berekend met de formule:
Voorbeeld :
In de Oxyz-ruimte is driehoek ABC gegeven met de coördinaten van drie hoekpunten A(-1;1;2), B(1;2;3), C(3;-2;0). Bereken de oppervlakte van driehoek ABC.
Oplossing :
Wij hebben:
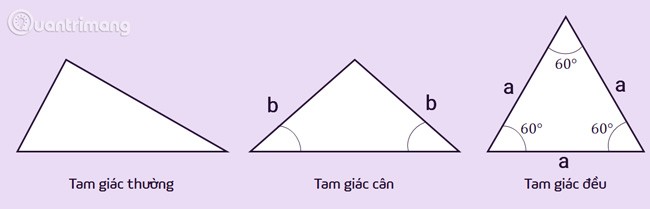
Om de oppervlakte van een driehoek te berekenen, moet u bepalen wat voor soort driehoek het is. Van daaruit vindt u de juiste formule voor oppervlakteberekening en de benodigde factoren om zo snel mogelijk de oppervlakte van een driehoek te berekenen.
Regelmatige driehoek: dit is de meest eenvoudige driehoek, heeft verschillende zijdelengtes en verschillende binnenhoeken. Regelmatige driehoeken kunnen ook speciale gevallen van driehoeken bevatten.
Gelijkbenige driehoek: een driehoek met twee gelijke zijden, deze twee zijden worden de twee zijkanten genoemd. Het hoekpunt van een gelijkbenige driehoek is het snijpunt van twee aangrenzende zijden. De hoek die door het toppunt wordt gevormd, wordt de tophoek genoemd, de andere twee hoeken heten de basishoeken. Een eigenschap van een gelijkbenige driehoek is dat de twee hoeken aan de basis gelijk zijn.
Gelijkzijdige driehoek: is een speciaal geval van een gelijkbenige driehoek waarbij alle drie de zijden gelijk zijn. De eigenschap van een gelijkzijdige driehoek is dat deze 3 gelijke hoeken heeft en een hoek van 60 graden is.
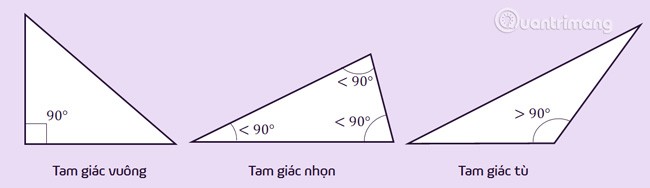
Rechthoekige driehoek: een driehoek met één hoek gelijk aan 90 graden (een rechte hoek).
Stompe driehoek: een driehoek met een binnenhoek groter dan 90° (een stompe hoek) of een buitenhoek kleiner dan 90° (een scherpe hoek).
Scherpe driehoek: een driehoek met drie binnenhoeken die allemaal kleiner zijn dan 90° (drie scherpe hoeken) of met alle buitenhoeken groter dan 90° (zes stompe hoeken).
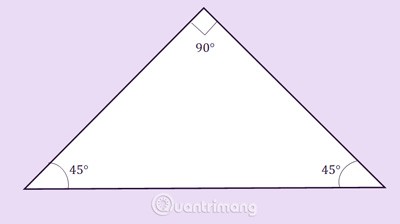
Gelijkbenige driehoek: is zowel een rechthoekige als een gelijkbenige driehoek.
Hierboven vindt u een samenvatting van veelgebruikte formules voor het berekenen van de driehoeksoppervlakte in het oxyz-coördinatensysteem. Als u zorgen, vragen of bijdragen hebt, laat dan hieronder een reactie achter om dit met Quantrimang.com te bespreken.
In dit artikel leggen we je uit hoe je weer toegang krijgt tot je harde schijf als deze kapot is. Laten we het artikel volgen!
Op het eerste gezicht lijken AirPods op alle andere echt draadloze oordopjes. Maar dat veranderde allemaal toen een paar onbekende functies werden ontdekt.
Apple heeft iOS 26 geïntroduceerd: een grote update met een gloednieuw matglasontwerp, slimmere ervaringen en verbeteringen aan bekende apps.
Studenten hebben een specifiek type laptop nodig voor hun studie. Deze moet niet alleen krachtig genoeg zijn om goed te presteren in hun studierichting, maar ook compact en licht genoeg om de hele dag mee te nemen.
Het toevoegen van een printer aan Windows 10 is eenvoudig, hoewel het proces voor bekabelde apparaten anders is dan voor draadloze apparaten.
Zoals u weet, is RAM een zeer belangrijk hardwareonderdeel van een computer. Het fungeert als geheugen voor de verwerking van gegevens en is de factor die de snelheid van een laptop of pc bepaalt. In het onderstaande artikel laat WebTech360 u zien hoe u met behulp van software in Windows RAM-fouten kunt opsporen.
Smart-tv's hebben de wereld veroverd. Dankzij zoveel geweldige functies en internetverbinding heeft technologie de manier waarop we televisiekijken veranderd.
Koelkasten zijn vertrouwde apparaten in huishoudens. Koelkasten hebben meestal twee compartimenten. Het koelvak is ruim en heeft verlichting die automatisch aangaat wanneer de gebruiker het vak opent. Het vriesvak is smal en heeft geen verlichting.
Wi-Fi-netwerken worden niet alleen beïnvloed door routers, bandbreedte en interferentie, maar er zijn een aantal slimme manieren om uw netwerk te versterken.
Als u terug wilt naar de stabiele iOS 16 op uw telefoon, vindt u hier de basisgids voor het verwijderen van iOS 17 en downgraden van iOS 17 naar 16.
Yoghurt is een heerlijk voedingsmiddel. Is het goed om elke dag yoghurt te eten? Hoe verandert je lichaam als je elke dag yoghurt eet? Laten we het samen ontdekken!
In dit artikel worden de meest voedzame rijstsoorten besproken en hoe u de gezondheidsvoordelen van de rijst die u kiest, optimaal kunt benutten.
Een slaapschema en bedtijdroutine opstellen, uw wekker verzetten en uw dieet aanpassen zijn enkele maatregelen die u kunnen helpen om beter te slapen en 's ochtends op tijd wakker te worden.
Huren alstublieft! Landlord Sim is een simulatiespel voor mobiel op iOS en Android. Je speelt als verhuurder van een appartementencomplex en begint met het verhuren van een appartement. Je doel is om het interieur van je appartement te verbeteren en het gereed te maken voor huurders.
Ontvang de Roblox-gamecode voor Bathroom Tower Defense en wissel deze in voor geweldige beloningen. Ze helpen je bij het upgraden of ontgrendelen van torens met hogere schade.
