De formule voor het berekenen van de oppervlakte en de omtrek van een parallellogram is basiskennis. Raadpleeg de formule die Quantrimang.com hieronder heeft samengesteld.
Inhoudsopgave
1. Oppervlakte van het parallellogram
De oppervlakte van een parallellogram wordt gemeten aan de hand van het oppervlak; het zichtbare vlakke gedeelte van het parallellogram.
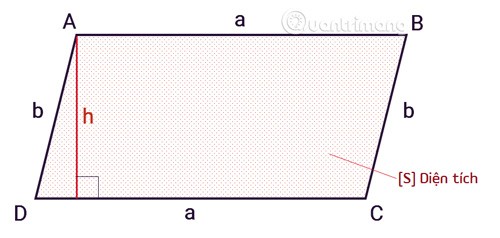
De oppervlakte van een parallellogram wordt berekend met de formule die gelijk is aan het product van de basis maal de hoogte.
SABCD = axh
Daarin:
Sis de oppervlakte van een parallellogram.ais de basis van het parallellogram.his de hoogte van een parallellogram, gemeten vanaf de bovenkant tot aan de basis.
2. Omtrek van parallellogram
De omtrek van een parallellogram wordt berekend door de lengte van de lijnen rondom de vorm (die ook de lijn rondom het gehele oppervlak vormen) op te tellen. Deze lengte is gelijk aan 2 keer de som van elk paar aangrenzende zijden.
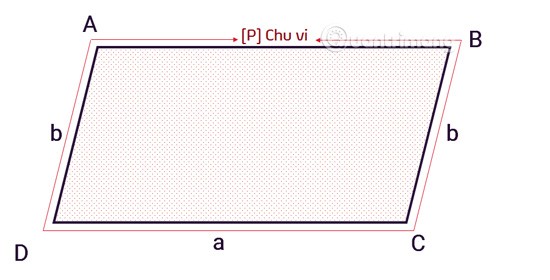
Met andere woorden: de omtrek van een parallellogram is de som van de lengtes van de vier zijden. De specifieke formule is als volgt:
C = 2x (a+b)
Daarin:
Cis de omtrek van een parallellogram.aen bzijn aaneengesloten zijden van een parallellogram.
3. Wat is een parallellogram?
Definiëren
Een parallellogram is een vierhoek met 2 paar evenwijdige zijden of 1 paar evenwijdige zijden. Een parallellogram heeft twee gelijke, tegenover elkaar liggende hoeken en twee diagonalen die elkaar in het midden van de vorm snijden.
Het parallellogram kan beschouwd worden als een speciaal geval van de trapezium.
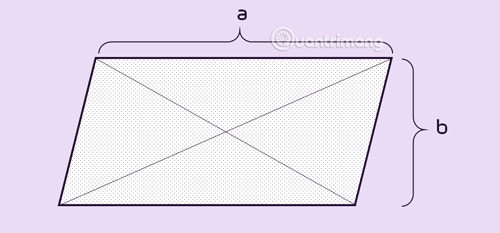
Eigenschappen van parallellogram
In parallellogram:
- De tegenoverliggende zijden zijn gelijk.
- Tegenoverliggende hoeken zijn gelijk.
- Twee diagonalen kruisen elkaar in het midden van elke lijn.
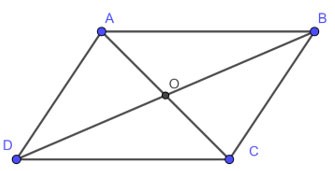
ABCD is een parallellogram, AC snijdt BD in O. Dan:
• AB = CD, AD = BC
•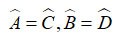
• OA = OC, OB = OD
Tekenen van herkenning
a) Een vierhoek waarvan de overstaande zijden evenwijdig zijn, is een parallellogram.
b) Een vierhoek met gelijke overstaande zijden is een parallellogram.
c) Een vierhoek met twee tegenoverliggende zijden die evenwijdig en gelijk zijn, is een parallellogram.
d) Een vierhoek met overstaande hoeken die gelijk zijn aan elkaar, is een parallellogram.
e) Een vierhoek met twee diagonalen die elkaar in het midden snijden, is een parallellogram.
4. Meerkeuzevragen om parallellogrammen te herhalen
Oefening 1 : Kies de verkeerde zin.
A. Een parallellogram bestaat uit twee diagonalen die elkaar in het midden van elke diagonaal snijden.
B. Parallellogram heeft twee gelijke tegenoverliggende hoeken
C. Een parallellogram heeft twee diagonalen die loodrecht op elkaar staan.
D. Twee parallellogrammen hebben twee paar evenwijdige, tegenoverliggende zijden.
Oplossing
In parallellogram:
+ Parallellogram heeft tegenoverliggende zijden evenwijdig
+ Tegenoverliggende zijden zijn gelijk
+ Twee diagonalen kruisen elkaar in het midden van elke lijn, dus C is onjuist.
Het juiste antwoord is: C
Oefening 2 : Gegeven parallellogram ABCD met  = α > 900. Teken buiten het parallellogram gelijkzijdige driehoeken ADE, ABF. Wat voor soort driehoek is driehoek CEF? Kies het beste antwoord
A. Driehoek
B. Gelijkbenige driehoek
C. Gelijkzijdige driehoek
D. Stompe driehoek
Antwoord:
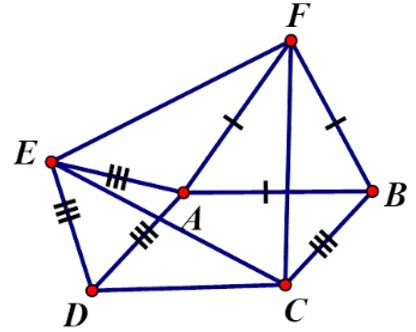

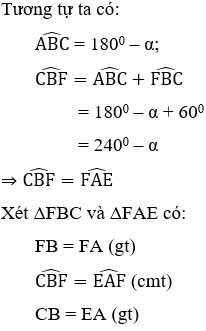
⇒ ΔFBC = ΔFAE (cgc) ⇒ CF = FE (2)
Uit (1) en (2) kunnen we afleiden dat CF = FE = EC, dus driehoek CEF is gelijkzijdig.
Les 3 : Kies de verkeerde zin. ABCD is een parallellogram. Dan:
A. AB = CD
B. n.Chr. = v.Chr.
C. Parallellogramtoets met antwoorden
D. AC = BD
Oplossing
In parallellogram:
+ Parallellogram heeft tegenoverliggende zijden evenwijdig
+ Tegenoverliggende zijden zijn gelijk
+ Twee diagonalen kruisen elkaar in het midden van elke lijn, dus D is onjuist.
Les 4 : Vul de lege plek in met de juiste zin: “Een vierhoek met twee diagonalen… is een parallellogram.”
A. gelijk
B. kruisen
C. snijden elkaar in het midden van elke lijn
D. parallel
Oplossing
Tekenen:
Een vierhoek met twee diagonalen die elkaar in het midden snijden, is een parallellogram.
Les 5 : Kies de verkeerde zin:
A. Een vierhoek met twee paar evenwijdige, tegenoverliggende zijden is een parallellogram.
B. Een trapezium met twee gelijke hoeken grenzend aan een basis is een parallellogram.
C. Een vierhoek met twee paar gelijke, tegenoverliggende zijden is een parallellogram.
D. Een vierhoek met twee paar gelijke, tegenover elkaar liggende hoeken is een parallellogram.
Oplossing
Tekenen:
+ Een vierhoek met tegenoverliggende evenwijdige zijden is een parallellogram, dus A is correct.
+ Een vierhoek met gelijke overstaande zijden is een parallellogram, dus D is correct.
+ Een vierhoek met overstaande hoeken die gelijk zijn aan elkaar, is een parallellogram, dus D is correct.
Als je beseft dat een trapezium met twee gelijke hoeken die aan de basis grenzen een gelijkbenige trapezium is, is B dus onjuist.
Het juiste antwoord is: B
5. Voorbeelden van het berekenen van de omtrek en oppervlakte van een parallellogram
Voorbeeld 1 : Gegeven een parallellogram met een basis van 12 cm, een zijde van 7 cm en een hoogte van 5 cm. Bereken de omtrek en oppervlakte van dat parallellogram.
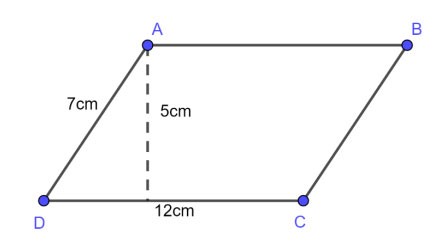
Prijs:
De omtrek van het parallellogram is:
P = 2 x (12 + 7) = 38 (cm)
De oppervlakte van een parallellogram is:
S = axh = 12 x 5 = 60 (cm2)
Voorbeeld 2:
Gegeven parallellogram ABCD met H en K als de voeten van de hoogtelijnen getekend vanaf de hoekpunten A, C tot en met BD.
a) Bewijs dat AHCK een parallellogram is.
b) Laat O het midden van HK zijn. Bewijs dat A, O, C collineair zijn.
Instructie:
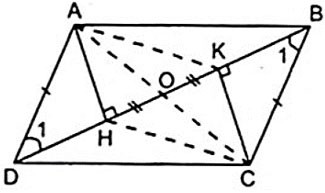
a) Vanuit de hypothese hebben we:
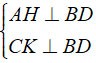 ⇒ AH//CK. ( 1 )
⇒ AH//CK. ( 1 )
Als we de eigenschappen van zijden van parallellogrammen en eigenschappen van afwisselende hoeken toepassen, krijgen we:
 ⇒ Δ ADH = Δ CBK
⇒ Δ ADH = Δ CBK
(hypotenusa – geval van een scherpe hoek)
⇒ AH = CK (overeenkomstige zijden zijn gelijk) ( 2 )
Uit (1) en (2) blijkt dat de vierhoek AHCK met de tegenoverliggende zijden evenwijdig en gelijk is, een parallellogram.
b) Pas de eigenschappen van de diagonalen van het parallellogram AHCK toe
Het parallellogram AHCK heeft twee diagonalen AC en HK die elkaar in het midden van elke lijn snijden. Omdat O het middelpunt van HK is, is O ook het middelpunt van AC.
⇒ A, O, C liggen op een rechte lijn.
Naast parallellogrammen zijn ook de formules voor het berekenen van de oppervlakte en de omtrek van andere veelvoorkomende geometrische vormen, zoals ruiten , vierkanten , trapeziums , rechthoeken ... van groot belang en worden ze veel gebruikt in de studie en het leven.
Hopelijk heeft u door bovenstaand artikel de basiskennis over parallellogrammen beter begrepen en begrepen. Als u vragen of opmerkingen heeft die u met Quantrimang.com wilt bespreken, kunt u hieronder een reactie achterlaten.




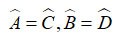



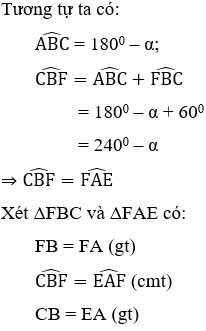


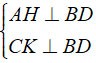 ⇒ AH//CK. ( 1 )
⇒ AH//CK. ( 1 ) ⇒ Δ ADH = Δ CBK
⇒ Δ ADH = Δ CBK