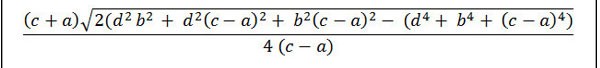Formule voor het berekenen van de oppervlakte van een trapezium: regelmatig, vierkant, gelijkbenig

Een trapezium is een convexe vierhoek met twee evenwijdige zijden, de basissen genoemd, en de overige zijden, de zijkanten. De formule voor het berekenen van de omtrek en oppervlakte van een trapezium behoort tot de basiskennis van de wiskunde die veelvuldig wordt toegepast in zowel de studie als het leven. Het volgende artikel introduceert de formule voor het berekenen van de oppervlakte van een trapezium en de lengte van de basis van een trapezium. Raadpleeg hiervoor het artikel.

Inhoudsopgave

• Formule voor het berekenen van de oppervlakte van een trapezium
  • Formule voor het berekenen van de oppervlakte van een trapezium als je 4 zijden kent (gevorderde opgave)
• Hoe bereken je de oppervlakte van een vierkante trapezium?
• Hoe bereken je de oppervlakte van een gelijkbenige trapezium?
• Bereken de lengte van de basis van de trapezium
• Soorten wiskunde om de oppervlakte van een trapezium te berekenen

Formule voor het berekenen van de oppervlakte van een trapezium

Er bestaat een trapezium ABCD met basis AB lengte a, basis CD lengte b en hoogte h.

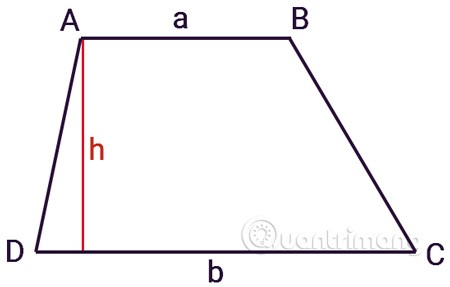
De oppervlakte van een trapezium is gelijk aan het gemiddelde van de twee bases vermenigvuldigd met de hoogte tussen de twee bases.

Daarin:

• S is de oppervlakte van het trapezium.
• a en b zijn de lengtes van de twee basisranden.
• h is de hoogte van basisrand a tot b of omgekeerd (afstand tussen 2 basisranden).

Er is ook een gedicht over het berekenen van de oppervlakte van een trapezium dat vrij gemakkelijk te onthouden is en wel als volgt:

Wilt u de oppervlakte van een trapezium berekenen?

We tellen de grote bodem en de kleine bodem bij elkaar op.

Optellen en vermenigvuldigen met de hoogte

Verdeel het in tweeën en neem het in tweeën, het komt er toch wel uit.

Formule voor het berekenen van de oppervlakte van een trapezium als je 4 zijden kent (gevorderde opgave)

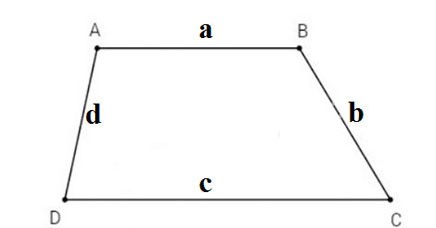
Als de opgave gegevens geeft over de lengte van 4 zijden, waarbij de basiszijden a en c duidelijk worden vermeld, waarbij basiszijde c groter is dan basiszijde a, en de zijkanten b en d zijn, dan kunt u de oppervlakte van de trapezium berekenen met behulp van de volgende formule.

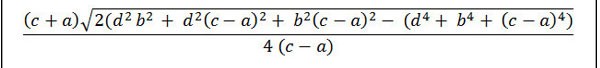
Daarin:

• S: Gebied
• a: kleine basis
• c: grote basisrand
• b, d: zijden van trapezium

Hoe bereken je de oppervlakte van een vierkante trapezium?

Een recht trapezium is een trapezium met één rechte hoek. De zijde die loodrecht op de twee bases staat, is tevens de hoogte h van het trapezium.

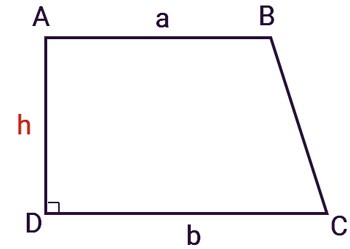
De algemene formule voor het berekenen van de oppervlakte van een rechte trapezium is vergelijkbaar met die van een regelmatige trapezium: het gemiddelde van de twee basiszijden vermenigvuldigd met de hoogte tussen de twee basissen . De hoogte is in dit geval echter de zijde die loodrecht op beide basissen staat.

Daarin:

• S is de oppervlakte van het trapezium.
• a en b zijn de lengtes van de twee basisranden.
• h is de lengte van de zijde die loodrecht op de twee bases staat.

Hoe bereken je de oppervlakte van een gelijkbenige trapezium?

Een gelijkbenige trapezium is een trapezium waarvan de twee aangrenzende hoeken gelijk zijn. De twee zijden van een trapezium zijn gelijk en niet evenwijdig aan elkaar.

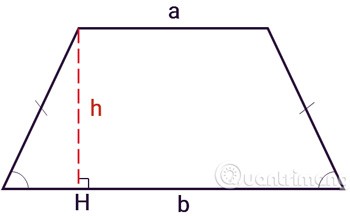
Naast het toepassen van de gebruikelijke formule om een ​​trapezium te berekenen, kun je de gelijkbenige trapezium ook in kleinere delen verdelen om de oppervlakte van elk deel te berekenen, en deze vervolgens bij elkaar optellen.

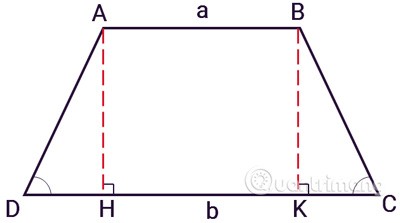
Bijvoorbeeld, de gelijkbenige trapezium ABCD heeft twee gelijke zijden AD en BC. Met de hoogtes AH en BK wordt het trapezium verdeeld in 1 rechthoek ABKH en 2 driehoeken ADH en BCK. Pas de formule toe voor het berekenen van de oppervlakte van een rechthoek voor ABHK en de oppervlakte van een driehoek voor ADH en BCK en tel vervolgens alle oppervlaktes bij elkaar op om de oppervlakte van trapezium ABCD te vinden.

Meer specifiek zoals dit:

En SADH = SBCK (gemakkelijk te bewijzen), dan krijgen we:

Bereken de lengte van de basis van de trapezium

Wanneer u de oppervlakte, hoogte en lengte van één zijde van de basis kent, kunt u de lengte van de resterende zijde als volgt berekenen:

Soorten wiskunde om de oppervlakte van een trapezium te berekenen

Voorbeeld 1: Bereken de oppervlakte van een trapezium

Bereken de oppervlakte van een trapezium, wetende dat de lengtes van de twee basissen respectievelijk 18 cm en 14 cm zijn; hoogte is 9 cm

Prijs: 

Als we de formule voor het berekenen van de oppervlakte van een trapezium toepassen, krijgen we:

De oppervlakte van de trapezium is dus 144 cm2

Voorbeeld 2: 

Er is een trapeziumvormig stuk land met een kleine basis van 24m en een grote basis van 30m. Breid de twee bases aan de rechterkant van het land uit, waarbij de grootste basis 7 m toevoegt en de kleinere basis 5 m toevoegt. Zo ontstaat een nieuw trapeziumvormig land met een oppervlakte die 36 m2 groter is dan de oorspronkelijke oppervlakte. Bereken de oppervlakte van het oorspronkelijke trapeziumvormige perceel.

Prijs:

Volgens de opgave is het vergrote oppervlak gelijk aan de oppervlakte van een trapezium met een grote basis van 7 m en een kleine basis van 5 m. De hoogte van het trapeziumvormige perceel is dus: h = (36 x 2) : (7 + 5) = 6 m

Het initiële landoppervlak is: S = 6. (24 + 30) : 2 = 162m²

Les 3:

Gegeven een recht trapezium met een afstand tussen de twee bases van 16 cm, is de kleine basis driekwart van de grote basis. Bereken de lengte van de 2 bases als je weet dat de oppervlakte van de rechte trapezium 112 cm² bedraagt.

Prijs:

De afstand tussen de twee bases van een rechte trapezium is de hoogte van de trapezium, dus:

De totale lengte van de twee bases is (112 x 2): 16 = 14 cm

De lengte van de kleine basis noemen we a, de lengte van de grote basis b, en dan hebben we:

a + b = 14 en a = ¾ b

Dus a = 14 x 4: 7 = 8 cm

Daarom is de kleine basis 34/7 cm, de grote basis 64/7 cm.

Voorbeeld 4: Gelijkbenige trapezium ABCD (AB//CD) heeft AB = 5 cm, CD = 13 cm, AD = 5 cm. De oppervlakte van trapezium ABCD berekenen?

Prijs:

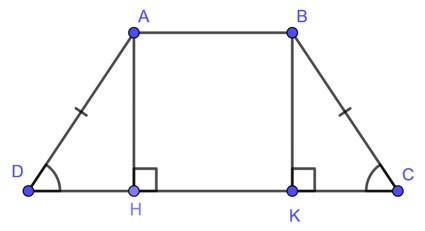
Laat AH en BK de twee hoogtes van het trapezium zijn. Dan is ABKH een rechthoek, we hebben:

Als we de stelling van Pythagoras toepassen op de rechthoekige driehoek AHD, krijgen we:

Dus: AH = 3cm

De oppervlakte van trapezium ABCD is dus:

Hierboven staat een artikel van Quantrimang.com over de meest standaardformule en manier om de oppervlakte van een trapezium te berekenen. Ik hoop dat dit artikel nuttig voor u is!