Formule voor het berekenen van het oppervlak en het volume van een bol

Laten we in het onderstaande artikel de formule voor het berekenen van de oppervlakte en het volume van een bol met Quantrimang.com leren en herhalen.

Inhoudsopgave

• Wat is een bol?
  • Wat is een bol?
• Formule voor het berekenen van het oppervlak en het volume van een bol
  • Formule voor het berekenen van het boloppervlak
  • Formule voor het berekenen van het volume van een bol:
• Formule voor het berekenen van de straal van een bol
  • De bol die de piramide omsluit heeft een zijde die loodrecht op de basis staat.
  • Vierkant tetraëder (dit is een speciaal geval van formule 1)
  • Een verticaal prisma heeft als basis een ingeschreven veelhoek.
  • Formule voor een tetraëder waarvan de hoekpunten de hoekpunten van een recht prisma zijn
  • Formule voor het berekenen van de straal van een bol voor een piramide met zijvlakken loodrecht op de basis
• Voorbeelden van het berekenen van het oppervlak en het volume van een bol

Wat is een bol?

Een bol is de verzameling punten die op gelijke afstand liggen van een gegeven vast punt O rin de driedimensionale ruimte. Punt O wordt het middelpunt genoemd en de afstand rwordt de straal van de bol genoemd.

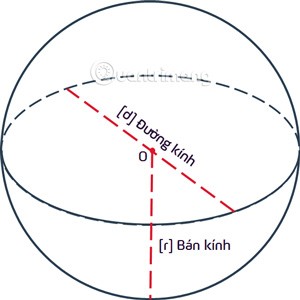
Wat is een bol?

Een bol is een verzameling punten die in een bol liggen. Een bol wordt een bol of bol genoemd met middelpunt O en straal r = OA.

Formule voor het berekenen van het oppervlak en het volume van een bol

Formule voor het berekenen van het boloppervlak

De oppervlakte van een bol is vier keer zo groot als de oppervlakte van een grote cirkel. Die oppervlakte is vier keer de constante Pi vermenigvuldigd met het kwadraat van de straal van de bol.

Formule voor het berekenen van het volume van een bol:

Het volume van een bol, ook wel het volume van een bol genoemd, wordt berekend door driekwart van Pi te vermenigvuldigen met de derde macht van de straal van de bol.

Daarin:

• Sis het oppervlak van de bol
• Vis het volume van een bol
• ris de straal van de bol/sfeer
• dis een bol/bol

Formule voor het berekenen van de straal van een bol

De bol die de piramide omsluit heeft een zijde die loodrecht op de basis staat.

• Rd is de straal van de basis.
• h is de lengte van de zijde loodrecht op de basis.

Bijvoorbeeld : Gegeven piramide S.ABCD met een rechthoekige basis met AB = 3a, BC = 4a, SA = 12a en SA loodrecht op de basis. Bereken de straal R van de bol die de piramide S.ABCD omschrijft.

Oplossing: We hebben

Dus

Vierkant tetraëder (dit is een speciaal geval van formule 1)

Het vierkante blok OABC heeft OA, OB, OC, loodrecht op elkaar en heeft:

Bijvoorbeeld:

Het tetraëder OABC heeft OA, OB, OC, die loodrecht op elkaar staan ​​en een omschreven bolvormige straal van . Het grootste volume van het tetraëder OABC

Oplossing : We hebben

Aan de andere kant hebben we:

Volgens de AM-GM ongelijkheid hebben we:

Een verticaal prisma heeft als basis een ingeschreven veelhoek.

Daarin:

• Rd is de straal van de basis
• h is de lengte van de zijde.

Voorbeeld 1: Gegeven een bol met straal R die een kubus met zijde a omschrijft. Welke van de volgende beweringen is waar?

A.

B.

C.

D.

Oplossing: We hebben

Het antwoord is dus C.

Formule voor een tetraëder waarvan de hoekpunten de hoekpunten van een recht prisma zijn

Het tetraëder (H1) heeft hoekpunten die de hoekpunten zijn van het verticale prisma (H2), dus:

Formule voor het berekenen van de straal van een bol voor een piramide met zijvlakken loodrecht op de basis

Waarin R, d de straal van de basis is; a, x zijn respectievelijk de lengte van het snijpunt van het zijvlak en de basis, de hoek aan de bovenkant van het zijvlak, kijkend naar de basis.

Of u kunt de formule gebruiken

Waarin: Rb de omgeschreven straal van het zijvlak is en a de lengte van het snijpunt van het zijvlak en de basis.

Bijvoorbeeld: 

Gegeven piramide S.ABCD met een vierkante basis, gelijkzijdige driehoek SAD met zijde √2a en liggend in een vlak loodrecht op de basis. Bereken de straal R van de bol die de piramide S.ABCD omschrijft.

A.

B.

Oplossing: We hebben

Het juiste antwoord is dus B.

Voorbeelden van het berekenen van het oppervlak en het volume van een bol

Les 1 : Gegeven een cirkel met een omtrek van 31,4 cm. Bereken het volume van een bol met een straal die gelijk is aan de straal van de gegeven cirkel.

Prijs:

Omtrek van cirkel C = 2πr = 31,4 cm

=> Straal r = C/2π = 5 cm

Het volume van de gegeven bol is:

V = ⁴⁄₃πr³ = 4/3.3.14.(5)³ = 523,3 cm³

Les 2 : Bereken het volume van een bol met diameter d = 4 cm.

Prijs:

Straal r = d/2 = 2 cm

Het volume van de bol is:

V = ⁴⁄₃πr³ = 4/3.3.14.(2)³ = 33,49 cm³

Les 3 :

Laat een cirkel met diameter 4a rond zijn diameter roteren. Wat is dan het volume van het roterende vaste lichaam?

Oplossing: Gegeven een cirkel met diameter 4a die om zijn diameter draait, krijgen we een bol met diameter 4a of straal R = 2a.

Het volume van de bol is:

Les 4 :

De bol met straal R√3 heeft een oppervlakte van:

A. 4√3πR2

B. 4πR2

C. 6πR2

D. 12πR2

Oplossing: Pas de formule toe: S = 4πR2

Het oppervlak van een bol met straal R√3 is: S = 4π(R√3)2 = 12πR2

Het antwoord is dus D.

Twee korte formules, maar ze lang onthouden is behoorlijk lastig. Markeer het artikel als favoriet en open het wanneer u het nodig hebt. Ik hoop dat dit artikel nuttig voor u is.

Naast de formule hierboven voor het berekenen van de oppervlakte en het volume van een bol, kunt u ook de formule raadplegen voor het berekenen van de oppervlakte van enkele andere basisvormen, zoals driehoeken , rechthoeken en parallellogrammen. ..