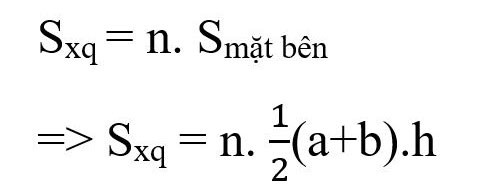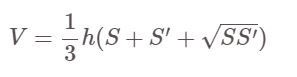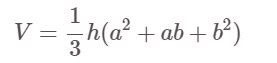Formule voor het berekenen van het volume van een afgeknotte piramide, het laterale oppervlak en het totale oppervlak van een afgeknotte piramide

Laten we in het onderstaande artikel leren wat een afgeknotte piramide is, hoe we het volume van een afgeknotte piramide, de zijdelingse oppervlakte en de totale oppervlakte van een afgeknotte piramide berekenen.

Inhoudsopgave

• Definitie van afgeknotte kegel
  • Eigenschappen van afgeknotte piramide:
• Formule voor het berekenen van de oppervlakte van een afgeknotte piramide
  • Oppervlakte van afgeknotte piramide 
  • Totale oppervlakte van een afgeknotte piramide
• Formule voor het berekenen van het volume van een afgeknotte piramide

Definitie van afgeknotte kegel

Een afgeknotte piramide is een deel van een veelvlak, gelegen tussen de basis en de doorsnede die doorsneden wordt door een vlak evenwijdig aan de basis van de piramide.

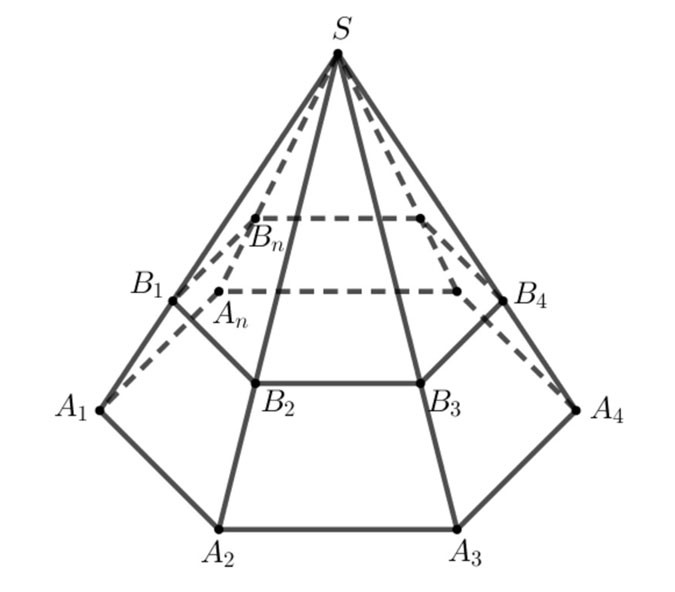
• De figuur bestaande uit de veelhoeken A1A2...An,B1B2...BnA1A2...An,B1B2...Bn en de trapeziums A1A2B2B1,A2A3B3B2,...,AnA1B1BnA1A2B2B1,A2A3B3B2,...,AnA1B1Bn wordt een afgeknotte piramide genoemd, aangeduid als A1A2...An.B1B2...Bn.A1A2...An.B1B2...Bn.
• Simpel gezegd wordt een afgeknotte piramide gevormd uit de piramide S.A1A2...AnS.A1A2...An nadat de piramide S.B1B2...Bn.S.B1B2...Bn is afgekapt.

+ De polygonen A1A2...An,B1B2...BnA1A2...An,B1B2...Bn worden de twee bases genoemd,

+ Trapeziums A1A2B2B1,A2A3B3B2,...,AnA1B1BnA1A2B2B1,A2A3B3B2,...,AnA1B1Bn worden laterale vlakken genoemd.

+ De lijnstukken A1B1,A2B2,...,AnBnA1B1,A2B2,...,AnBn worden de zijkanten genoemd, de randen van het basisoppervlak worden de basisranden genoemd.

+ De afstand tussen de twee bases wordt de hoogte van de afgeknotte piramide genoemd.

Eigenschappen van afgeknotte piramide:

• De twee bases zijn twee veelhoeken (driehoeken, vierhoeken, vijfhoeken, enz.) met overeenkomstige evenwijdige zijden en gelijke verhoudingen van overeenkomstige zijden.
• De zijkanten zijn allemaal trapeziumvormig.
• De lijnen die de laterale randen bevatten, komen samen in een punt (de top van de piramide).
• Een afgeknotte piramide is een piramide waarvan de grondvlakken regelmatige veelhoeken zijn (met gelijke zijden). Daarom zijn alle zijkanten van een afgeknotte kegel gelijke trapeziums.

Formule voor het berekenen van de oppervlakte van een afgeknotte piramide

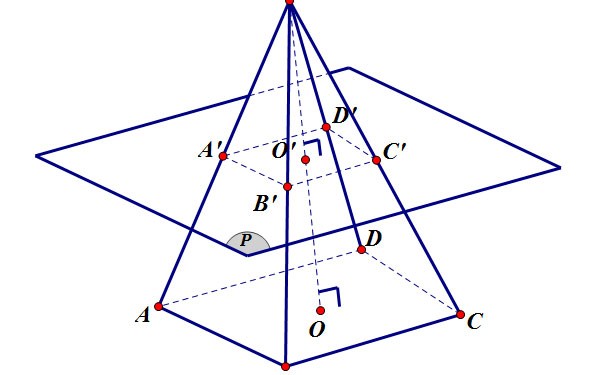
Oppervlakte van afgeknotte piramide

Het zijvlak van een afgeknotte piramide is het oppervlak van de omliggende vlakken, het deel dat de afgeknotte piramide omgeeft, exclusief het oppervlak van de twee bases.

Hoe bereken je de oppervlakte van de zijkant van een afgeknotte piramide? Bereken de oppervlakte van elk zijvlak (trapezium) van de afgeknotte piramide volgens de formule voor de berekening van de oppervlakte van een normale trapezium en bereken vervolgens de totale oppervlakte.

Formule voor het berekenen van de oppervlakte van een regelmatige afgeknotte piramide:

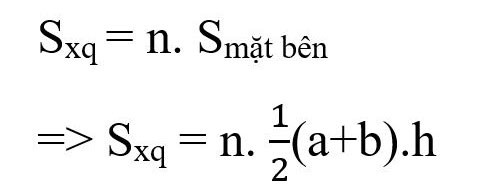
Daarin:

• Sxq: omgeving
• n: aantal zijvlakken van de afgeknotte piramide (gelijk aan het aantal randen van de basispolygoon)
• a, b: zijlengtes van respectievelijk de bovenste en onderste basis
• h: hoogte van de zijdevierhoeken.

Voorbeeld 1: 

Bereken de oppervlakte van de zijkant van een regelmatige vierhoekige afgeknotte piramide met de ribben aan de basis 10 cm en 15 cm en de hoogte van de zijden 12 cm.

Prijs: 

De zijkant van een regelmatige vierhoekige afgeknotte piramide is een gelijkbenige trapezium, dus de oppervlakte van één zijkant is:

Een regelmatige vierhoekige afgeknotte piramide heeft 4 gelijke zijden, dus de manteloppervlakte is:

150 x 4 = 600 (cm2)

Voorbeeld 2: Bereken de oppervlakte van de mantel van een regelmatige vierzijdige afgeknotte piramide met de ribben van de basis van 6 cm en 8 cm en de hoogte van de zijden van 5 cm. Bereken de oppervlakte van de mantel van een regelmatige vierzijdige afgeknotte piramide met basisranden van 6 cm en 8 cm.

Prijs: 

De zijkant van een regelmatige vierhoekige afgeknotte piramide is een gelijkbenige trapezium, dus de oppervlakte van één zijkant is gelijk aan

Een regelmatige vierhoekige afgeknotte piramide heeft vier gelijke zijden, dus het laterale oppervlak is gelijk aan

35 x 4 = 140 (cm2)

Totale oppervlakte van een afgeknotte piramide

De totale oppervlakte van een afgeknotte piramide is gelijk aan de som van de oppervlakte van de zijkant en de oppervlakte van de twee bases.

Formule:                    Stp = Sxq + Grote bodem + Kleine bodem

Daarin:

• Stp: Totale oppervlakte
• Sxq: Omgeving
• Grote basis: Groot basisoppervlak
• Kleine basis: Klein basisoppervlak

Bijvoorbeeld: 

Bereken de totale oppervlakte van een regelmatige afgeknotte piramide volgens de afmetingen in de afbeelding.

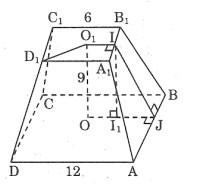
Prijs:

Wij hebben:

AD = 12 ⇒ OJ = 6

Teken II1 ⊥ OJ, we hebben: I1J = 3

Als we de stelling van Pythagoras toepassen op rechthoekige driehoek II1J, dan krijgen we:

IJ2 = II12 + I1J2 = 92 + 32 = 90

Vandaar:

De oppervlakte van één zijde van een trapezium is:

De omgeving is gelijk aan:

De oppervlakte van de bovenste basis is: S = 6 x 6 = 36 (eenheden)

De oppervlakte van de onderkant is: S = 12 x 12 = 144 (eenheden)

De totale oppervlakte van een afgeknotte piramide is gelijk aan:

Formule voor het berekenen van het volume van een afgeknotte piramide

Recept:

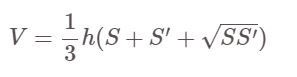
Daarin:

• V: volume van de afgeknotte piramide
• S, S' zijn respectievelijk de oppervlakten van de grote en kleine basis van de piramide.
• h: hoogte van de piramide, dat is de afstand tussen de twee grote en kleine bases

Is een afgeknotte piramide een vierkant (regelmatige vierhoek):

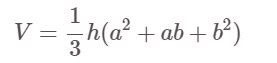
Daarin:

• V: Volume
• h: Hoogte van de piramide
• a, b zijn respectievelijk de lengtes van de randen van de grote en de kleine basis.