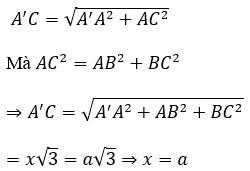Een prisma is een veelhoek met twee evenwijdige grondvlakken en twee parallellogramzijvlakken.
Opmerking:
- De zijkanten van een prisma zijn gelijk en evenwijdig aan elkaar.
- De zijkanten zijn parallellogrammen.
- De twee bases van een prisma zijn twee gelijke veelhoeken.
Wat is de formule voor het berekenen van het volume van een prisma (V-prisma) en wat is de formule voor het berekenen van het volume van een verticaal prisma? Zie onderstaand artikel.
Inhoudsopgave
1. Volume van een verticaal prisma
Formule voor het berekenen van het volume van een verticaal prisma:
Het volume van een recht prisma is gelijk aan het product van de oppervlakte van de basis vermenigvuldigd met de hoogte.
Daarbinnen
Vis het volume van het prisma (eenheid m3)Bis het basisoppervlak (eenheid m2)his de hoogte van het prisma (eenheid m)
3. Classificatie van prisma's
Regelmatig prisma
Een verticaal prisma met een regelmatige veelhoek als basis. De zijkanten van het prisma zijn allemaal gelijke rechthoeken. Bijvoorbeeld: regelmatig driehoekig prisma, regelmatige vierhoek... dan begrijpen we het als een regelmatig prisma.
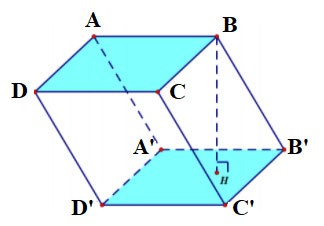
Een regelmatige vierhoek met als basis een regelmatig vierhoekprisma.
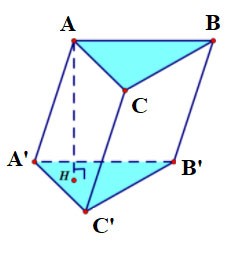
Driehoekig prisma
- Een driehoekig prisma heeft 5 vlakken, 9 ribben en 6 hoekpunten.
- De twee bases zijn beide driehoekig en evenwijdig aan elkaar; Elke zijkant is een rechthoek;
- De zijden zijn gelijk;
- De hoogte van een driehoekig prisma is gelijk aan de lengte van één zijde.
Bijvoorbeeld:
Het driehoekige prisma ABC.A'B'C' heeft:
- De onderste basis is driehoek ABC, de bovenste basis is driehoek A'B'C';
De zijkanten zijn rechthoeken: AA'B'B, BB'C'C, CC'A'A;
- Randen:
- Basisranden: AB, BC, CA, A'B', B'C', C'A'
- Zijden: AA', BB', CC';
- Hoekpunten: A, B, C, A', B', C'.
- Hoogte is de lengte van één zijde: AA' of BB' of CC'.
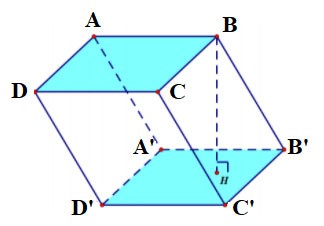
Vierhoekig prisma
- Een vierzijdig prisma heeft 6 vlakken, 12 ribben en 8 hoekpunten.
- De twee basissen zijn beide vierhoeken en evenwijdig aan elkaar. Elke zijde is een rechthoek.
- De zijden zijn gelijk.
- De hoogte van een vierzijdig prisma is gelijk aan de lengte van één zijde.
Bijvoorbeeld:
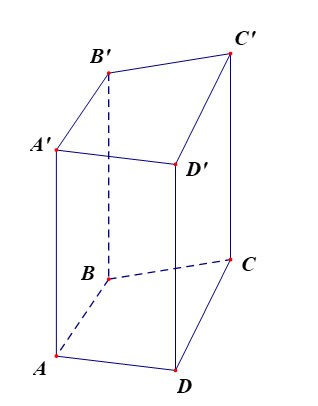
Vierzijdig prisma ABCD.A'B'C'D' heeft:
- De onderste basis is vierhoek ABCD, de bovenste basis is vierhoek A'B'C'D';
De zijkanten zijn rechthoeken: AA'B'B, BB'C'C, CC'D'D, DD'A'A;
- Randen:
+ Basisranden: AB, BC, CD, DA, A'B', B'C', C'D', D'A'
+ Zijkanten: AA', BB', CC', DD' zijn gelijk.
- Hoekpunten: A, B, C, D, A', B', C', D'.
- Hoogte is de lengte van één zijde: AA' of BB' of CC' of DD'.
Let op: Rechthoekige prisma's en kubussen zijn ook vierzijdige prisma's.
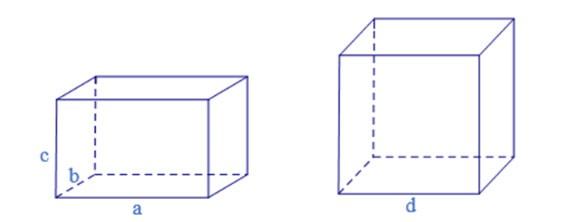
Rechter prisma
Wanneer de zijkanten van een prisma loodrecht op de basis staan, wordt het een recht prisma genoemd.
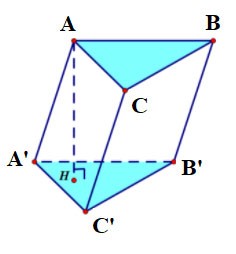
Opmerking:
Als de basis een rechthoek is, wordt de verticale cilinder van de vierhoek een rechthoekige doos genoemd.
Als een vierhoekige cilinder 12 zijden heeft met lengte a, dan wordt hij een kubus genoemd.
Vergelijk het rechter prisma en het gewone prisma:
| DEFINIËREN: |
NATUUR |
| + Een verticaal prisma is een prisma met een zijde loodrecht op de basis. |
+ De zijkanten van een verticaal prisma zijn rechthoekig.
+ De zijkanten van het prisma staan loodrecht op het basisvlak.
+ Hoogte is de zijkant
|
| + Een regelmatig prisma is een verticaal prisma waarvan de basis een regelmatige veelhoek is. |
+ De zijkanten van een prisma zijn allemaal gelijke rechthoeken.
+ Hoogte is de zijkant
|
4. Voorbeeld van het berekenen van het volume van een verticaal prisma
Voorbeeld 1:
Gegeven prisma ABC.A'B'C' met basis ABC als gelijkzijdige driehoek met zijde a = 2 cm en hoogte h = 3 cm. Bereken het volume van dit prisma.
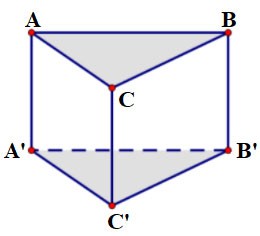
Prijs:
Omdat de basis een gelijkzijdige driehoek is met zijde a, is de oppervlakte:
Op dit moment is het volume van het prisma:
Voorbeeld 2:
Oefening 1: Gegeven een verticale doos met randen AB = 3a, AD = 2a, AA'= 2a. Bereken het volume van blok A'.ACD'
Instructie:
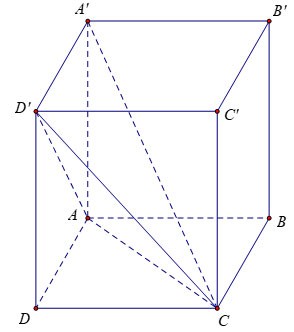
Omdat de zijkant ADD'A' een rechthoek is, geldt:
Voorbeeld 3 : Gegeven een verticaal prisma ABC.A'B'C' waarvan de basis een gelijkzijdige driehoek is met zijde a√3, is de hoek tussen de basis en het prisma 60º. Laat M het midden van BB' zijn. Bereken het volume van de piramide M.A'B'C'.
Prijs:
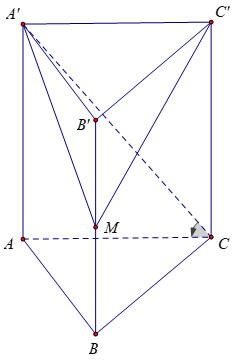
Daarom kunnen we afleiden dat
Wij hebben:
Voorbeeld 4:
Gegeven een regelmatig vierhoekig prisma ABCD.A'B'C'D' met een basisribbe van lengte a en vlak (DBC') dat een hoek van 60º maakt met basis ABCD. Bereken het volume van prisma ABCD.A'B'C'D?
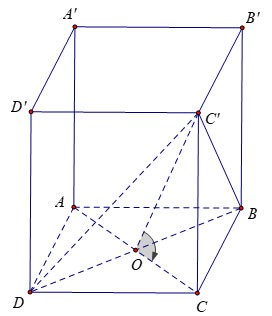
We hebben: in het middelpunt O van vierkant ABCD.
Aan de andere kant dus
Afleiden
Ook:
Voorbeeld 5:
Bereken het volume V van kubus ABCD.A'B'C'D', wetende dat AC'=a√3
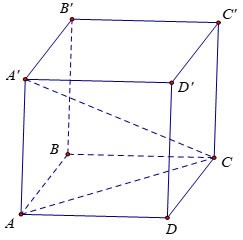
Prijs:
Zij x de lengte van de zijde van de kubus.
Beschouw driehoek AA'C met een rechte hoek in A, met:
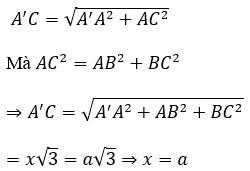
Het volume van de kubus is dus V=a^3.
Naast de formule voor het berekenen van het volume van een prisma hierboven, kunt u ook meer artikelen raadplegen over de formule voor het berekenen van het volume van een omwentelingslichaam , de formule voor het berekenen van de oppervlakte en de omtrek van een cirkel ...