Hexadecimale en decimale systemen
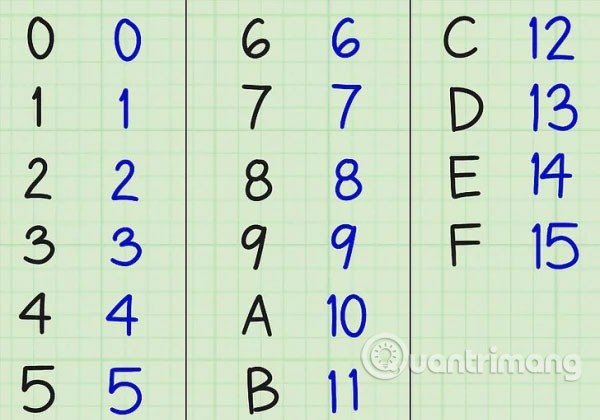
Hexadecimaal heeft 16 cijfers. De cijfers 1 tot en met 9 zijn hetzelfde als in het decimale stelsel. De decimale getallen 10 tot en met 15 worden echter vervangen door de letters A, B, C, D, E en F uit het Engelse alfabet.
Het decimale stelsel (ook wel bekend als het 10-tallig stelsel) is het standaardstelsel voor het weergeven van gehele getallen en niet-gehele getallen (decimale getallen). Dit is een uitbreiding voor niet-gehele getallen van het Hindoe-Arabische getallenstelsel.
Hoe je grondtal 16 naar grondtal 10 converteert
Hexadecimaal is een getallensysteem met grondtal 16 en decimaal is een getallensysteem met grondtal 10. Soms moeten we het decimale equivalent van een hexadecimaal getal weten.
Hier zijn de stappen om van 16-tallig naar 10-tallig te converteren:
Hier is een voorbeeld:
7DE is een hexadecimaal getal
7DE = 2014 (in decimaal)
Voorbeeld van het omrekenen van 16- naar 10-tallig stelsel:
Conversietabel van basis 16 naar basis 10
| Hexadecimaal systeem | Basis 10-systeem |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| A | 10 |
| B | 11 |
| C | 12 |
| D | 13 |
| E | 14 |
| F | 15 |
Zie ook:
In dit artikel leggen we je uit hoe je weer toegang krijgt tot je harde schijf als deze kapot is. Laten we het artikel volgen!
Op het eerste gezicht lijken AirPods op alle andere echt draadloze oordopjes. Maar dat veranderde allemaal toen een paar onbekende functies werden ontdekt.
Apple heeft iOS 26 geïntroduceerd: een grote update met een gloednieuw matglasontwerp, slimmere ervaringen en verbeteringen aan bekende apps.
Studenten hebben een specifiek type laptop nodig voor hun studie. Deze moet niet alleen krachtig genoeg zijn om goed te presteren in hun studierichting, maar ook compact en licht genoeg om de hele dag mee te nemen.
Het toevoegen van een printer aan Windows 10 is eenvoudig, hoewel het proces voor bekabelde apparaten anders is dan voor draadloze apparaten.
Zoals u weet, is RAM een zeer belangrijk hardwareonderdeel van een computer. Het fungeert als geheugen voor de verwerking van gegevens en is de factor die de snelheid van een laptop of pc bepaalt. In het onderstaande artikel laat WebTech360 u zien hoe u met behulp van software in Windows RAM-fouten kunt opsporen.
Smart-tv's hebben de wereld veroverd. Dankzij zoveel geweldige functies en internetverbinding heeft technologie de manier waarop we televisiekijken veranderd.
Koelkasten zijn vertrouwde apparaten in huishoudens. Koelkasten hebben meestal twee compartimenten. Het koelvak is ruim en heeft verlichting die automatisch aangaat wanneer de gebruiker het vak opent. Het vriesvak is smal en heeft geen verlichting.
Wi-Fi-netwerken worden niet alleen beïnvloed door routers, bandbreedte en interferentie, maar er zijn een aantal slimme manieren om uw netwerk te versterken.
Als u terug wilt naar de stabiele iOS 16 op uw telefoon, vindt u hier de basisgids voor het verwijderen van iOS 17 en downgraden van iOS 17 naar 16.
Yoghurt is een heerlijk voedingsmiddel. Is het goed om elke dag yoghurt te eten? Hoe verandert je lichaam als je elke dag yoghurt eet? Laten we het samen ontdekken!
In dit artikel worden de meest voedzame rijstsoorten besproken en hoe u de gezondheidsvoordelen van de rijst die u kiest, optimaal kunt benutten.
Een slaapschema en bedtijdroutine opstellen, uw wekker verzetten en uw dieet aanpassen zijn enkele maatregelen die u kunnen helpen om beter te slapen en 's ochtends op tijd wakker te worden.
Huren alstublieft! Landlord Sim is een simulatiespel voor mobiel op iOS en Android. Je speelt als verhuurder van een appartementencomplex en begint met het verhuren van een appartement. Je doel is om het interieur van je appartement te verbeteren en het gereed te maken voor huurders.
Ontvang de Roblox-gamecode voor Bathroom Tower Defense en wissel deze in voor geweldige beloningen. Ze helpen je bij het upgraden of ontgrendelen van torens met hogere schade.
