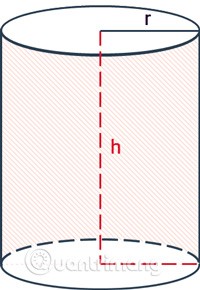
Laten we de formule voor het berekenen van de laterale oppervlakte, totale oppervlakte en hoogte van een cilinder leren kennen. Deze formule kunnen we gebruiken tijdens onze studie en in het dagelijks leven.
Inhoudsopgave
Hoe bereken je de oppervlakte van een cilinder?
De oppervlakte van een cilinder bestaat uit het laterale oppervlak en het totale oppervlak.
U kunt de hoogte en de straal van de cilinder in de onderstaande tabel invoeren om het laterale oppervlak en het totale oppervlak van de cilinder te weten te komen.
Formule voor het berekenen van het laterale oppervlak van een cilinder
De oppervlakte van de mantel van een cilinder omvat alleen de oppervlakte van het omringende oppervlak van de cilinder, niet de oppervlakte van de twee bodems.
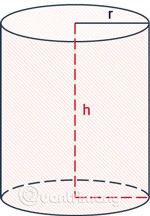
De formule voor het berekenen van de oppervlakte van de cilinder is de omtrek van de basiscirkel vermenigvuldigd met de hoogte.
 |
Daarin:
- Omgeving is de omgeving.
ris de straal van de cilinder.his de hoogte, de afstand tussen de twee bases van de cilinder.
|
Voorbeeld: 1
Een cirkelvormige cilinder heeft een basisstraal r = 5 cm en een hoogte h = 7 cm. Bereken de zijdelingse oppervlakte van een verticale cilinder.
Oplossing: Oppervlakte van een cirkelvormige cilinder: Sxq = 2.π.rh = 2π.5,7 = 70π = 219,8 (cm2).
Voorbeeld: 2
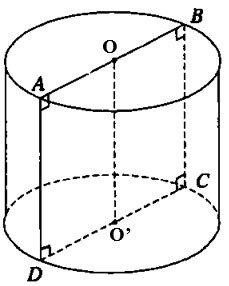
Gegeven vierkant ABCD met zijde 2a. Laat O en O' respectievelijk de middens zijn van de zijden AB en CD. Wanneer we dat vierkant om de OO'-as draaien, ontstaat er een roterende cilinder. Bereken het oppervlak van de draaiende cilinder.
Oplossing:
De straal van de basiscirkel is r = CD = a
De hoogte van de cilinder is h= OO'= AD=2a
Het laterale oppervlak van de cilinder is dus Sxq = 2πrh = 2π.a.2a = 4a2π
Formule voor het berekenen van de totale oppervlakte van een cilinder
Het totale oppervlak wordt berekend als de grootte van de gehele ruimte die door de figuur wordt ingenomen, inclusief het laterale oppervlak en het oppervlak van de twee cirkelvormige bases.
De formule voor het berekenen van de totale oppervlakte van een cilinder is de oppervlakte van de zijkant plus de oppervlakte van de twee bases.
Voorbeeld 1 : Bereken de totale oppervlakte van een cilinder met basis 3 en hoogte 5.
Oplossing:
Het totale oppervlak is Stp = Sxq + 2Sd = 2πr(r+h) = 2π.3(3+5) = 48π
Bereken de hoogte van de cilinder
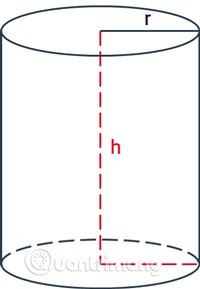
De hoogte van een cilinder is de afstand tussen de twee bases van de cilinder.
Bereken de hoogte van een cilinder als je de totale oppervlakte en de basisstraal kent
Bijvoorbeeld: Gegeven een cilinder met basisstraal R = 8 cm en totale oppervlakte 564π cm2. Bereken de hoogte van de cilinder.
Prijs:
Wij hebben
Bereken de hoogte van een cilinder als je het laterale oppervlak kent
=>
Formule voor het berekenen van de straal van de basis van een cilinder
1. Formule voor het berekenen van de omtrek van een cirkel; oppervlakte van een cirkel
Cirkel heeft omtrek C=2πr
=>
De cirkel met de basis heeft oppervlakte S=πr2
=>
Bijvoorbeeld. Bereken de straal van de cilinderbasis in de volgende gevallen:
A. De omtrek van de basiscirkel is 6π
B. De oppervlakte van de basis is 25π
Oplossing:
A. De straal van de basiscirkel is
B. De straal van de basiscirkel is
2. De basis is de cirkel die in de veelhoek is ingeschreven
- Ingeschreven in een willekeurige driehoek: waarbij S de oppervlakte van de driehoek is en p de halve omtrek
- Ingeschreven in een gelijkzijdige driehoek: zijde
- Ingeschreven vierkant:
Voorbeeld 1 . Gegeven een ingeschreven cilinder in een kubus met ribbe a. Bereken de straal van de cilinder.
De straal van de cilinder is:
Voorbeeld 2 . Gegeven een regelmatig prisma ABC.A'B'C' met , het volume omschreven rond de cilinder. Bereken de straal van de cilinder.
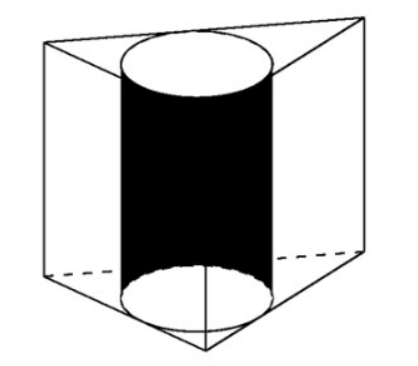
Het volume van het prisma is
De basis van een regelmatig prisma is een gelijkzijdige driehoek, dus => de zijde
De straal van de cilinderbasis is dus:
3. De basis is de cirkel die de veelhoek omschrijft.
Omschreven in een willekeurige driehoek:
Daarin:
- a, b, c zijn de lengtes van de drie zijden van de driehoek
- p is de halve omtrek van de driehoek:
Omtrek van een rechthoekige driehoek: hypotenusa
Omtrek van gelijkzijdige driehoek: zijde
Omtrek van het vierkant: zijde
Bijvoorbeeld:
Bereken de basisstraal van de cilinder die de regelmatige piramide S.ABC omschrijft in de volgende gevallen:
A. ABC is een rechthoekige driehoek in A met AB = a en AC = a√3
B. ABC heeft AB= 5; AC= 7; BC=8
Prijs:
A. Hypotenusa
Omdat ABC een rechte hoek is in A, is de straal R=0,5.BC=a
B. De halve omtrek van driehoek ABC is
Wat is een cirkelvormige cilinder?
Een cirkelvormige cilinder is een cilinder met twee gelijke, cirkelvormige bases die evenwijdig aan elkaar liggen.
Cilinders worden veel gebruikt in zowel eenvoudige als complexe geometrische problemen, waarbij de formule voor het berekenen van de oppervlakte en het volume van cilinders vaak op verschillende manieren wordt gebruikt. Als je al weet hoe je de oppervlakte en de omtrek van een cirkel kunt berekenen, kun je gemakkelijk de formules afleiden voor het berekenen van het volume, de omtrek en de totale oppervlakte van een cilinder.
Formule voor het berekenen van de dwarsdoorsnede van een cilinder
Snijd de cilinder door het vlak (P) door de as
- De resulterende doorsnede is een rechthoek.
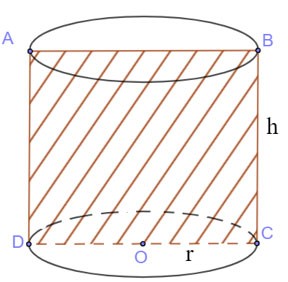 |
Dwarsdoorsnede:
SABCD = BC.CD = 2r.h
|
Snijd de cilinder door vlak (P) evenwijdig aan en op een afstand x van de as
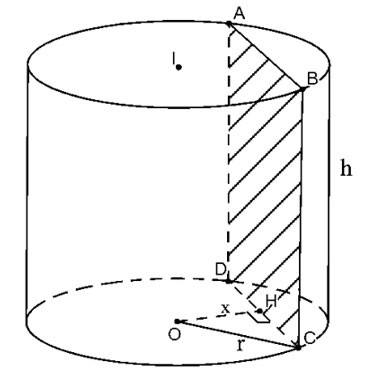 |
De resulterende doorsnede is rechthoek ABCD zoals hierboven weergegeven.
Laat H het midden van CD zijn, we hebben OH ⊥ CD=>
Daarom is de dwarsdoorsnede
|
Snijd de cilinder door vlak (P) niet loodrecht op de as, maar snijd alle generatoren van de cilinder door
 |
De gevormde doorsnede is een cirkel met middelpunt O' en straal O'A'=r
Dwarsdoorsnede: S = πr2
|
Snijd de cilinder door vlak (P) dat niet loodrecht op de as staat, maar snijd alle generatoren van de cilinder door.
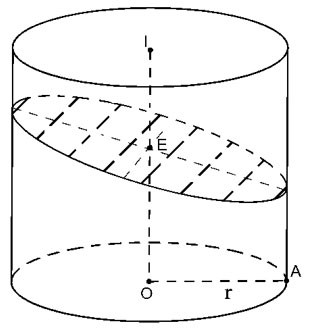 |
De resulterende doorsnede is een ellips (E) met kleine as 2r => a=r
Grote as is gelijk aan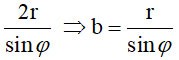
met 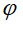 is de hoek tussen de OI-as en (P) is de hoek tussen de OI-as en (P)
Dus oppervlakte S= π. ab=
|
Voorbeeld van het berekenen van de oppervlakte van een cilinder
Les 1 :
De omtrek van de cilinder is 13 cm en de hoogte 3 cm.
Prijs:
We hebben: omtrek van cirkel C = 2R.π = 13cm, h = 3cm
Het laterale oppervlak van de cilinder is dus:
Sxq = 2πr.h = Ch = 13,3 = 39 (cm²)
Les 2 : Gegeven een cilinder met een straal van de basiscirkel van 6 cm, terwijl de hoogte van de basis tot de bovenkant van de cilinder 8 cm dik is. Wat is de laterale oppervlakte en de totale oppervlakte van de cilinder?
Prijs
Volgens de formule hebben we de basis van de halve cirkel r = 6 cm en de hoogte van de cilinder h = 8 cm. Daarom hebben we de formule om het laterale oppervlak van een cilinder en het totale oppervlak van een cilinder als volgt te berekenen:
Oppervlakte van de cilinder = 2 x π xrxh = 2 x π x 6 x 8 = ~ 301 cm²
Totale oppervlakte van de cilinder = 2 Π x R x (R + H) = 2 X π x 6 x (6 + 8) = ~ 527 cm²
Les 3 : Een cilinder heeft een grondvlakstraal van 7 cm en een manteloppervlak van 352 cm2.
De hoogte van de cilinder is dan:
(A) 3,2 cm; (B) 4,6 cm; (C) 1,8 cm
(D) 2,1 cm; (E) Een ander resultaat
Selecteer het juiste resultaat.
Oplossing: We hebben
Dus antwoord E is juist.
Les 4 : De hoogte van een cilinder is gelijk aan de straal van de basiscirkel. Het manteloppervlak van de cilinder bedraagt 314 cm2. Bereken de straal van de basiscirkel en het volume van de cilinder (rond de uitkomst af op twee decimalen).
Prijs:
Het laterale oppervlak van de cilinder is 314 cm2
We hebben Sxq = 2.π.rh = 314
Waar r = h
Dus 2πr² = 314 => r² ≈ 50 => r ≈ 7,07 (cm)
Volume van de cilinder: V = π.r2.h = π.r3 ≈ 1109,65 (cm³).
Hopelijk heeft het bovenstaande artikel u geholpen bij het verkrijgen van basis- en gevorderde kennis over cilinders en het berekenen van de totale oppervlakte en de zijdelingse oppervlakte van een cilinder.










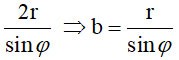
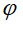 is de hoek tussen de OI-as en (P)
is de hoek tussen de OI-as en (P)