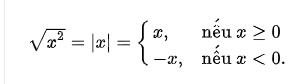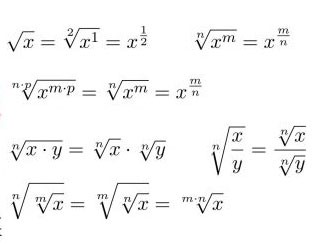Vierkantswortels zijn een van de belangrijkste onderdelen van wiskunde en worden tijdens het leerproces van leerlingen gebruikt. In het volgende artikel leggen we u uit wat een vierkantswortel is en hoe u de vierkantswortel van een getal berekent. Zie hiervoor.
Inhoudsopgave
Wat is een vierkantswortel?
De vierkantswortel van een getal a is een getal x, zodanig dat x2 = a, of met andere woorden, het getal x waarvan het kwadraat = a.
Bijvoorbeeld, 2 en −2 zijn vierkantswortels van 2, want 2² = (−2)² = 4.
Het wortelteken wordt aangegeven met √.
- Elk niet-negatief reëel getal a heeft een unieke niet-negatieve vierkantswortel, de rekenkundige kwadratische wortel.
De rekenkundige vierkantswortel van 16 is bijvoorbeeld 4, aangegeven door √16 = 4, omdat 4² = 4 × 4 = 16 en 4 een positief getal is.
Elk positief getal a heeft twee vierkantswortels: √a is een positieve vierkantswortel en −√a is een negatieve vierkantswortel. Ze worden gelijktijdig aangeduid met ± √a.
De meest elementaire vierkantswortelberekeningen
Onthoud een aantal basis- en meest voorkomende kwadraatgetallen, zodat u bij het worteltrekken sneller uit uw hoofd kunt rekenen:
0² = 0
1² = 1
3² = 9
4² = 16
5² = 25 6² = 36
7² = 49
8² = 64
9² =
81 10² =
100
11² = 121 12²
= 144
13² = 169
14² = 196
15² = 225
16² = 256
17² = 289
Hier volgen enkele basisformules voor vierkantswortels die iedereen zou moeten onthouden:
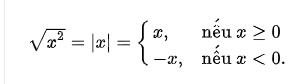
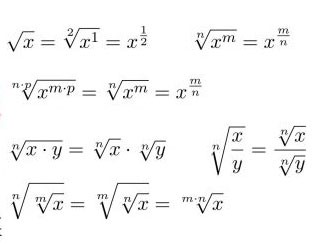
Vierkantsworteltabel
De vierkantsworteltabel is verdeeld in rijen en kolommen, waardoor u direct de vierkantswortel van getallen groter dan 1 en kleiner dan 100 kunt vinden.
De vierkantswortels van getallen met maximaal drie cijfers van 1,00 tot 99,9 staan in de tabel in kolom 0 tot en met 9. Hierna volgen negen correctiekolommen waarmee u het laatste cijfer van de vierkantswortels van getallen met vier cijfers van 1,000 tot 99,99 kunt corrigeren.
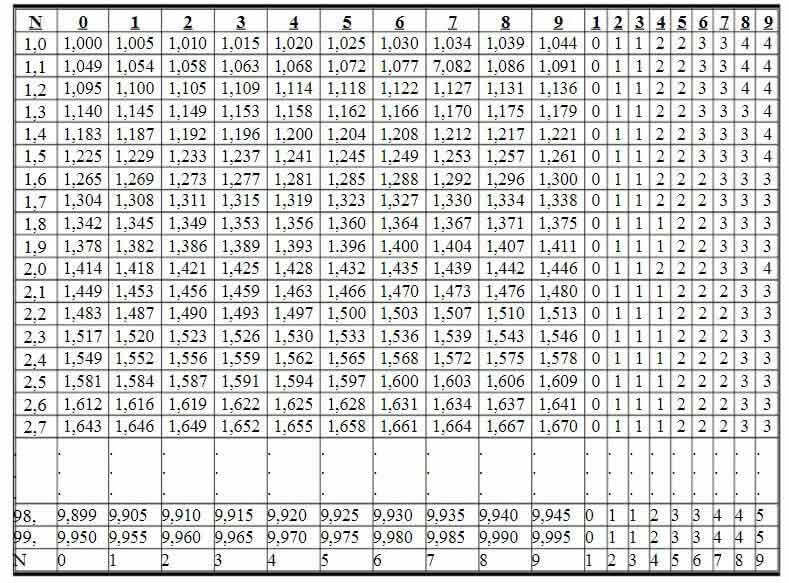
Voorbeeld 1: Vinden
→ Oplossing:
Op het kruispunt van rij 1,4 en kolom 1 zien we het getal 1,187
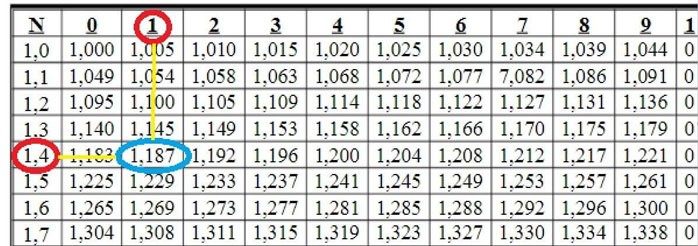
Dus
Voorbeeld 2:
Vinden
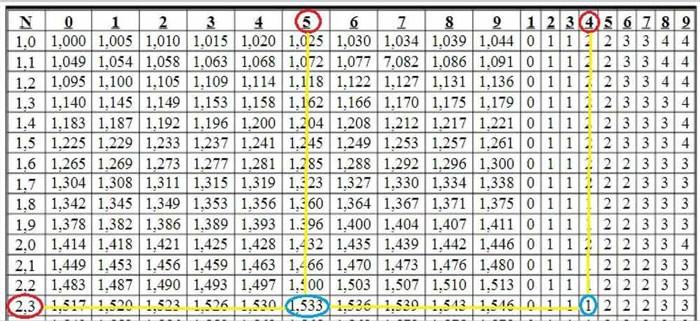
Op het snijpunt van rij 2, 3 en kolom 5 zien we het getal 1,533. Wij hebben
Vervolgens zien we op het kruispunt van rij 2, 3 en kolom 4 het getal 1. Dit getal 1 wordt gebruikt om het laatste cijfer van het getal te corrigeren. Dat is: 1,533 + 0,001 = 1,534
Dus
Hoe bereken je de vierkantswortel zonder rekenmachine?
De vierkantswortel van een geheel getal vinden
Bereken de vierkantswortel door vermenigvuldiging.
De vierkantswortel van een getal is het getal dat, wanneer je het getal met zichzelf vermenigvuldigt, het oorspronkelijke getal oplevert.
Dat betekent dus: "Welk getal kun je met zichzelf vermenigvuldigen om het getal te krijgen dat je al hebt?"
Bijvoorbeeld:
De vierkantswortel van 1 is 1, want 1 maal 1 is 1 (1 x 1 = 1).
De vierkantswortel van 4 is 2, want 2 maal 2 is 4 (2 x 2 = 4).
De vierkantswortel van 9 is 3, want 3 x 3 = 9.
Gebruik deling om de vierkantswortel te vinden
Om de vierkantswortel van een geheel getal te vinden, kunt u het gehele getal delen door opeenvolgende getallen totdat u een quotiënt vindt dat precies gelijk is aan uw deler.
Bijvoorbeeld:
16 gedeeld door 4 is 4, dus 4 is de vierkantswortel van 16.
4 gedeeld door 2 is 2, dus 2 is de vierkantswortel van 4.
Vind de vierkantswortel van andere getallen
Raad het en gebruik vervolgens het eliminatieproces.
Voorbeeld: Bereken de vierkantswortel van 20.
Ondertussen weten we dat 16 een perfect kwadraatgetal is met wortel 4 (4X4=16).
25 heeft ook een vierkantswortel van 5 (5X5=25).
Wij schatten dus dat de vierkantswortel van 20 ergens tussen 4 en 5 ligt.
We kunnen raden dat de vierkantswortel van 20 4,5 is en proberen 4,5 te kwadrateren om dit te controleren. Dat wil zeggen, neem 4,5 x 4,5. Als het antwoord niet 20 is, kijken we of de uitkomst groter of kleiner is dan 20 om de berekening uit te voeren. Als het getal kleiner is dan 20, dan proberen we het met 4, 6 en grotere getallen. Als de uitkomst groter is dan 20, probeer dan te rekenen met 4, 4 en kleinere getallen tot u de juiste uitkomst krijgt.
De uitkomst van deze berekening is 4,475 x 4,475 = 20,03. Als je naar beneden afrondt, is het antwoord 20.
Hoe vierkantswortels te vergelijken
Met twee positieve getallen a en b
Als a = b dan
Als a > b dan
Als een < b="" dan="">
Bijvoorbeeld:
Vergelijk en
Omdat 21 < 31,
Hopelijk heeft het bovenstaande artikel u geholpen bij het verkrijgen van kennis over vierkantswortels, hoe u moet rekenen, hoe u moet vergelijken... zodat u oefeningen over vierkantswortels en andere gerelateerde oefeningen kunt oplossen.