Wat is een rationaal getal? Wat is een irrationeel getal?

Definities en formules van rationale en irrationale getallen vormen belangrijke kennis binnen de wiskunde die leerlingen moeten begrijpen om een ​​solide wiskundige basis te hebben. In het onderstaande artikel leert u de definitie, eigenschappen en wiskundige vormen van rationale en irrationale getallen. Raadpleeg deze informatie.

Rationale getallen, irrationale getallen

• Wat is een rationaal getal?
  • Classificatie van rationale getallen
  • Het weergeven van rationale getallen op een getallenlijn
  • Optellen en aftrekken van rationale getallen
  • Vermenigvuldigen en delen van rationale getallen
  • Absolute waarde van een rationaal getal
  • Vergelijk twee rationale getallen
  • Formule voor het berekenen van de macht van een rationaal getal
• Wat is een irrationeel getal?
  • Het concept van irrationale getallen
  • Eigenschappen van irrationale getallen
• Wat is het verschil tussen rationale en irrationale getallen?
• Relatie van getallenreeksen
• Oefeningen op rationale getallen

Wat is een rationaal getal?

- Rationale getallen zijn de verzameling getallen die als breuken (quotiënten) kunnen worden geschreven. Dat wil zeggen dat een rationaal getal kan worden weergegeven als een oneindig repeterend decimaal.

- Rationale getallen worden geschreven als , waarbij a en b gehele getallen zijn, maar b niet 0 mag zijn.

- is de verzameling van rationale getallen.

=> Verzameling van rationale getallen: .

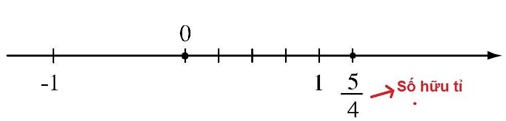
Bijvoorbeeld: , , … zijn rationale getallen.

• Elk geheel getal a is een rationaal getal, omdat het gehele getal a in de vorm kan worden geschreven.

Bijvoorbeeld: we hebben rationale getallen.

Wij hebben:

Commentaar: zijn allemaal rationale getallen.

Classificatie van rationale getallen

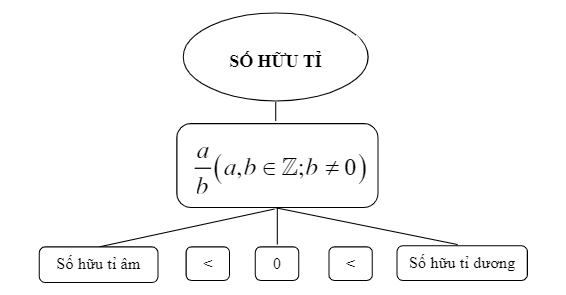
Rationale getallen worden onderverdeeld in twee typen: negatieve rationale getallen en positieve rationale getallen. Meer specifiek:

• Negatieve rationale getallen: omvatten rationale getallen kleiner dan 0.
• Positieve rationale getallen: omvatten rationale getallen groter dan 0.

Let op: het getal 0 is noch een negatief rationaal getal, noch een positief rationaal getal.

Natuur

• De verzameling van rationale getallen is een aftelbare verzameling.
• Commutatieve eigenschap:
• Opteleigenschap met 0:
• Gecombineerde eigenschappen:

Het weergeven van rationale getallen op een getallenlijn

- Om rationale getallen op de getallenlijn weer te geven, volgen we de volgende factoren:

Stap 1: Schrijf het rationale getal als een breuk

Stap 2: Verdeel het eenheidslijnsegment in gelijke delen om een ​​nieuw eenheidslijnsegment te krijgen dat de oude eenheid is.

Stap 3: Het rationale getal wordt weergegeven door punt A, dat een afstand van een nieuwe eenheid vanaf punt 0 voorstelt.

• A staat links van 0 als het een negatief getal is.
• A staat rechts van 0 als het een positief getal is.

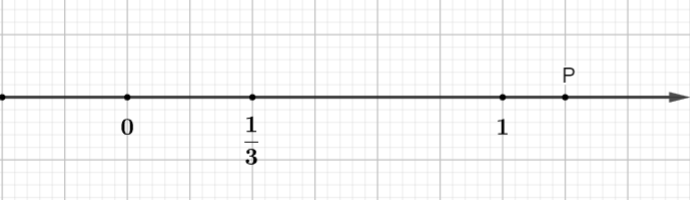
Bijvoorbeeld: In de figuur stelt punt P het rationale getal voor:

Instrueren

Het eenheidslijnsegment is verdeeld in 6 gelijke delen (de nieuwe eenheid is 1/6 van de oude eenheid)

Punt P ligt op een afstand van 7 nieuwe eenheden van punt O.

En punt P ligt rechts van punt O, dus P is een positief rationaal getal.

P stelt dus een rationaal getal voor.

Optellen en aftrekken van rationale getallen

i) Regels voor het optellen en aftrekken van twee rationale getallen

We kunnen twee rationale getallen x en y optellen en aftrekken door ze als twee breuken te schrijven en vervolgens de regels voor het optellen en aftrekken van breuken toe te passen.

Bij ons hebben wij:

ii) Eigenschappen

- Optellen van rationale getallen heeft de eigenschappen van optellen van breuken: commutatief, associatief, optellen met 0, optellen met tegengestelden.

- Wij hebben:

a) Commutatieve eigenschap:

b) Associatieve eigenschappen:

c) Tel 0 op:

d) Tel het tegengestelde getal op:

iii, Overgangsregels

Wanneer we een term van de ene kant van een vergelijking naar de andere kant verplaatsen, moeten we het teken van die term veranderen.

In Q hebben we een algebraïsche som, waarin we termen kunnen verwisselen en haakjes kunnen plaatsen om termen willekeurig te groeperen, net als algebraïsche sommen in de verzameling van gehele getallen.

• Met als dan
• Bij ons hebben wij:

Vermenigvuldigen en delen van rationale getallen

i) Regels voor het vermenigvuldigen en delen van twee rationale getallen

- We kunnen twee rationale getallen vermenigvuldigen en delen door ze als breuken te schrijven en vervolgens de regels voor het vermenigvuldigen en delen van breuken toe te passen.

• Bij ons hebben wij:
• Bij ons hebben wij:

Bijvoorbeeld:

Vermenigvuldig rationale getallen: 

Deel rationale getallen: 

ii) Eigenschappen

- Vermenigvuldiging van rationale getallen heeft ook dezelfde eigenschappen als vermenigvuldiging van breuken: commutatief, associatief, vermenigvuldiging met 1 en distributieve eigenschap van vermenigvuldiging boven optelling.

- Elk rationaal getal dat niet nul is, heeft een inverse.

- Wij hebben:

• Commutatieve eigenschap: .
• Associatieve eigenschappen: .
• Eigenschap van vermenigvuldigen met 1: .
• Distributieve eigenschappen: .
• Met . Het omgekeerde van a is .

Absolute waarde van een rationaal getal

- De absolute waarde van een rationaal getal a, aangegeven met , is de afstand van punt a tot punt 0 op de getallenlijn.

Bijvoorbeeld:

(Omdat )

(Omdat )

Vergelijk twee rationale getallen

- Bij 2 willekeurige rationale getallen is er altijd of of .

- Om twee rationale getallen te vergelijken doen we het volgende:

• Schrijf als 2 breuken met dezelfde positieve noemer:
• Vergelijk de tellers als gehele getallen a, b:

Bijvoorbeeld: Vergelijk twee rationale getallen: en

Wij hebben:

Omdat het goed is.

Formule voor het berekenen van de macht van een rationaal getal

Formules voor het berekenen van machten van rationale getallen die u moet onthouden

• Product van twee machten met dezelfde basis:
• Macht van macht
• Kracht van een product
• Macht van een quotiënt

Wat is een irrationeel getal?

Het concept van irrationale getallen

• Wanneer we het over rationale getallen hebben, kunnen we niet anders dan irrationele getallen noemen. Dit zijn getallen geschreven in de vorm van oneindige, niet-repeterende decimalen, aangegeven met .
• Reële getallen die geen rationale getallen zijn, kunnen niet als verhoudingen worden weergegeven.

Bijvoorbeeld: 3,145248… is een irrationeel getal.

Eigenschappen van irrationale getallen

De verzameling van irrationale getallen is een overtelbare verzameling.

Bijvoorbeeld:

Irrationale getallen: 0,10100100010000100000010000001… (dit is een oneindig, niet-repeterend decimaal)

Aantal vierkantswortels: √2 (vierkantswortel)

Pi (π): 3,14159 26535 89793 23846 26433 83279 50 288…..

Wat is het verschil tussen rationale en irrationale getallen?

• Rationale getallen omvatten niet-eindige repeterende decimalen, terwijl irrationale getallen niet-eindige, niet-repeterende decimalen zijn.
• Rationale getallen zijn gewoon breuken, terwijl irrationale getallen veel verschillende typen getallen kennen.
• Rationale getallen zijn telbare getallen, terwijl irrationale getallen ontelbare getallen zijn.

Relatie van getallenreeksen

Symbolen van getallenreeksen:

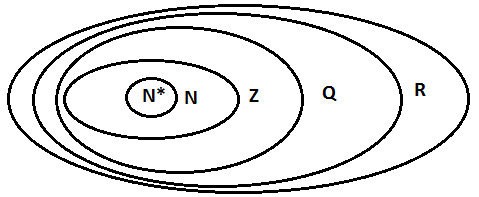
• N: Verzameling van natuurlijke getallen
• N*: verzameling natuurlijke getallen anders dan 0
• Z: verzameling gehele getallen
• V: De verzameling van rationale getallen
• I: Verzameling van irrationale getallen

Wij hebben: R = Q ∪ I.

Stel N in; Z ; Q; R.

Dan is de inclusierelatie tussen de verzamelingen getallen: N ⊂ Z ⊂ Q ⊂ R

Oefeningen op rationale getallen

Formulier 1: Berekeningen uitvoeren met rationale getallen

Oplossingsmethode: Om oefeningen op te lossen over het uitvoeren van berekeningen met rationale getallen, zet u eerst de rationale getallen om in breuken. Pas vervolgens de rekenregels toe op optellen, aftrekken, vermenigvuldigen en delen van rationale getallen.

Voorbeeld: Berekenen  

Antwoord:

Formulier 2: Het weergeven van rationale getallen op de getallenlijn

Oplossing: U moet bepalen of het rationale getal een positief of een negatief rationaal getal is en vervolgens doorgaan met de volgende stappen:

• Als het rationale getal a/b een positief rationaal getal is: Verdeel op de getallenlijn, in de positieve richting, de lengte van 1 eenheid in b gelijke delen. Neem vervolgens een punt op de positieve richting van de Os-as, wijs een deel aan en bepaal de positie van het rationale getal a/b.
• Als het rationale getal a/b een negatief rationaal getal is: Verdeel op de getallenlijn, in de negatieve richting van de as, de lengte van 1 eenheid in b gelijke delen. Neem vervolgens een punt op de negatieve richting van de Os-as, wijs een deel aan en bepaal de positie van het rationale getal a/b.

Formulier 3: Rationale getallen vergelijken

Oplossing: Zet de gegeven rationale getallen om in breuken met dezelfde positieve noemer en vergelijk vervolgens de tellers. Als we nog verder gevorderd zijn, kunnen we het vergelijken met tussenliggende breuken om het antwoord te vinden.

Formulier 4: Bepaal of een rationaal getal negatief, positief of 0 is

Oplossingsmethode: Om oefeningen van type 4 op te lossen, moeten leerlingen op basis van de eigenschappen van rationale getallen bepalen of het rationale getal negatief, positief of 0 is.

Bijvoorbeeld: Gegeven het rationale getal x = (a – 25)/29, bepaal de waarde van a zodat:

• x is negatief
• x is positief
• x = 0

Antwoord:

x is een negatief getal => (a – 25)/29 < 0=""> a – 25 < 0=""> a <>

x is een positief getal => (a – 25)/29 > 0 => a – 25 > 0 => a > 25

x = 0 => (a – 25)/29 = 0 0 => a – 25 = 0 => a = 25

Formulier 5: Vind rationale getallen in het interval volgens gegeven voorwaarden

Oplossing: Als de vraag vereist dat we rationale getallen binnen een interval berekenen volgens gegeven voorwaarden, moeten we de rationale getallen in dezelfde teller of noemer plaatsen om het antwoord te vinden.

Voorbeeld: Vind de waarde van m voor groter dan en kleiner dan

Antwoordgids

Zet breuken als volgt om naar gemeenschappelijke delers:

Gemeenschappelijke deler: 18

Volgens de vraag hebben we:

Formulier 6: Vind x met rationale getallen

Methode om wiskundige problemen op te lossen: Om wiskundige problemen x met rationale getallen te vinden, is het nodig om een ​​gemeenschappelijke delerreductie uit te voeren en x naar één kant te converteren, en de resterende termen naar 1. Bereken hieruit de waarde van x

Bijvoorbeeld: Bereken x als u x kent. (2/3) + 5/6 = 1/8

Antwoord:

X . (2/3) + 5/6 = 1/8

=> x . (2/3) = 1/8 + 5/6

=> x = 46/ 48 : 2/ 3

=> x = 23 . 3 / 24 . 2

=> 23/16

Formulier 7: Vind a zodat de uitdrukking een geheel getal is

Methode voor het oplossen van wiskundige problemen: Voor het probleem van het vinden van a, als de teller geen a bevat, moeten we het deelbaarheidsteken gebruiken. Als de teller a bevat, gebruik dan het deelbaarheidsteken of scheid de teller door de noemer. Als het probleem vereist dat u zowel a als b tegelijkertijd moet berekenen, groepeert u a of b en zet u ze voor de berekening om in breukvorm.

Voorbeeld: Zoek het gehele getal a met de voorwaarde dat 8/(a – 1) een geheel getal is

Antwoord:

Voorwaarde: a – 1 ≠ 0 => a ≠ 1

Laat a een geheel getal zijn => 8 is deelbaar door (a – 1)

=> (a – 1) is een factor 8 => U(8) = {-8, -4, -2, -1, 1, 2, 4, 8}

=> (a – 1) = {-8, -4, -2, -1, 2, 4, 8}

=> a = {-7, -3, -1, 0, 3, 5, 9}

Hopelijk heeft het bovenstaande artikel u geholpen bij het begrijpen wat rationale getallen zijn, wat irrationele getallen zijn, welke soorten rationale getallen er zijn, wat symbolen voor rationale getallen zijn en hoe u rationale getallen kunt herkennen om problemen eenvoudig op te lossen.

Naast de kennis over irrationale getallen en rationale getallen hierboven, kunt u verwijzen naar andere wiskundige kennis, zoals breuken , gemengde getallen , decimalen ...