Wat is een reëel getal?

Wat zijn reële getallen? Welke getallen behoren tot de verzameling van reële getallen? Lees het onderstaande artikel om deze belangrijke wiskundige kennis beter te begrijpen.

Reëel getal

• 1. Wat is een reëel getal?
• 2. Reële getallen-as
•  3. Vergelijk reële getallen
• 3. Eigenschappen van de verzameling reële getallen
• 4. Absolute waarde van een reëel getal
• 5. Voorbeeldoefeningen met reële getallen

1. Wat is een reëel getal?

• Reële getallen zijn de verzameling van rationale getallen en irrationele getallen.
• Set is het symbool voor de verzameling van reële getallen, die bestaat uit reële getallen.

• Een rationaal getal is een getal geschreven als een breuk (a, b ∈ Z, b ≠ 0). Bijvoorbeeld 
• De verzameling rationale getallen wordt aangeduid met 
• Een irrationeel getal is een oneindig, niet-repeterend decimaal getal. Bijvoorbeeld:
• De verzameling irrationale getallen wordt aangeduid met 

De verzameling van reële getallen beslaat de getallenlijn.

Bijvoorbeeld:

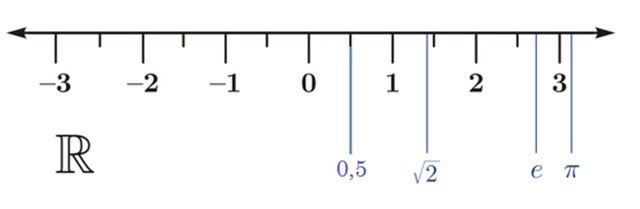
2. Reële getallen-as

Elk reëel getal wordt weergegeven door een punt op de getallenlijn.

• Omgekeerd stelt elk punt op de getallenlijn een reëel getal voor.
• Alleen de verzameling van reële getallen vult de getallenlijn.

 3. Vergelijk reële getallen

Methode

• Bij twee reële getallen x en y geldt altijd x = y of x < y of x > y
• Reële getallen groter dan 0 worden positieve reële getallen genoemd, reële getallen kleiner dan 1 worden negatieve reële getallen genoemd. Het getal 0 is noch een positief, noch een negatief reëel getal.
• Het vergelijken van positieve reële getallen is vergelijkbaar met het vergelijken van rationale getallen.
• Als a en b twee positieve reële getallen zijn, geldt: als a > b, dan is .

Voorbeeld: Vul het juiste cijfer in het vakje in:

Oplossingsgids

a) -7,5(0)8 > -7,513

b) -3,02 <>

c) -0,4(9)854 <>

d) -1,(9)0765 <>

Voorbeeld: Reële getallen ordenen: van klein naar groot

Oplossingsgids

Rangschik de reële getallen van klein naar groot:

Bijvoorbeeld: Bewijs dat:

Met a en b zijn twee positieve reële getallen. Als a > b, dan

Oplossingsgids

Als a > b dan

a, b zijn twee positieve reële getallen, dus a + b > 0

Als a > b dan is a – b > 0

Overweeg het product

Omdat a2 – b2 > 0

=> a2 > b2 => dpcm

3. Eigenschappen van de verzameling reële getallen

In de verzameling definiëren we ook de bewerkingen optellen, aftrekken, vermenigvuldigen, delen, machtsverheffen, worteltrekken... En in de bewerkingen hebben de reële getallen ook dezelfde eigenschappen als de bewerkingen in de verzameling van de rationale getallen.

In de verzameling van reële getallen hebben bewerkingen de volgende eigenschappen met betrekking tot vermenigvuldiging:

• Voor alle eigendommen:
• Voeg 0 toe: 
• Commutatieve eigenschap: ;
• Gecombineerde eigenschappen: 
• Commutatieve eigenschap: a. b = b. A
• Associatieve eigenschappen: (a. b). c = a. (b.c)
• Eigenschappen van vermenigvuldiging met getal 1:
• Distributieve eigenschap van vermenigvuldiging over optelling: a. (b + c) = a. b + a. C
• Voor elk reëel getal a ≠ 0 is er een inverse zodat

- Dat wil zeggen dat de bovenstaande berekeningen net als andere getallenreeksen commutatieve en associatieve eigenschappen hebben. En hetzelfde geldt voor aftrekken, vermenigvuldigen, delen…

Relatie tussen getallenreeksen

Bijvoorbeeld: Voer de berekening uit:

Oplossingsgids

Bijvoorbeeld: bepaal x, wetende:

Oplossingsgids

4. Absolute waarde van een reëel getal

Definitie: De afstand van punt a tot punt 0 op de getallenlijn is de absolute waarde van een getal a (a is een reëel getal). De absolute waarde van een negatief getal is zichzelf, de absolute waarde van een negatief getal is zijn tegengestelde.

Overzicht:

• Als
• Als
• Als
• Als

Natuur

• De absolute waarde van elk getal is niet-negatief.
• Algemeen: voor alle a ∈ R

Meer specifiek:

Sommige eigenschappen

- Twee getallen die gelijk of tegengesteld zijn, hebben dezelfde absolute waarde. En omgekeerd: twee getallen die dezelfde absolute waarde hebben, zijn gelijk of tegengesteld.

Overzicht:

- Elk getal is groter dan of gelijk aan het tegenovergestelde van zijn absolute waarde en tegelijkertijd kleiner dan of gelijk aan zijn absolute waarde.

Overzicht: en

- Van twee negatieve getallen heeft het kleinste getal de grootste absolute waarde.

Overzicht: Als

- Van twee positieve getallen heeft het kleinste getal de kleinste absolute waarde.

Overzicht: Als

- De absolute waarde van een product is gelijk aan het product van de absolute waarden.

Overzicht:

- De absolute waarde van een quotiënt is gelijk aan het quotiënt van twee absolute waarden.

Overzicht:

5. Voorbeeldoefeningen met reële getallen

Voorbeeld 1: Vul de lege plekken in met de juiste symbolen ∈, ∉, ⊂ (…):

3 …. Q; 3 …. R ; 3… ik; -2,53… V;

0,2(35) …. I ; N …. Z ; I …. R.

Instrueren

a) 3 ∈ Q ; 3 ∈ R ; 3 ∉ ik ; -2,53 ∈ Q

b) 0,2(35) ∉ I ; N ∈ Z ; Ik ⊂ R

Voorbeeld 2: Vind de sets

a) Q ∩ I ;
b) R ∩ I.

Instrueren

a) Q ∩ I = Ø ;
b) R ∩ I = I.

Voorbeeld 3: Vul het juiste cijfer in tussen (…) 

a) – 3,02 < –="" 3,="" …="">

b) – 7,5 … 8 > – 7,513

c) – 0,4 … 854 < –="">

d) -1, … 0765 < –="">

Instrueren

a) – 3,02 < –="">
b) – 7.508 > – 7.513 ;
c) – 0,49854 < –="" 0,49826="">
d) -1,90765 < –="">

Voorbeeld 4: Vind x, wetende:

3,2.x + (-1,2).x +2,7 = -4,9;

Instrueren

3.2. x + (-1,2).x + 2,7 = -4,9

[3,2 + (-1,2)].x + 2,7 = -4,9.

2.x + 2,7 = – 4,9.

2.x = – 4,9 – 2,7

2.x = – 7,6

x = -7,6 : 2

x = -3,8

Naast reële getallen kun je hier ook meer leren over andere definities in de wiskunde, zoals kwadratische getallen , irrationele getallen, rationale getallen , priemgetallen , natuurlijke getallen ...