Het middelpunt van een driehoek is het snijpunt van de drie hoogtelijnen . Dat wil zeggen dat het snijpunt van de lijnen van elk hoekpunt van de driehoek naar de tegenoverliggende zijde een rechte hoek vormt. De lengte van de hoogte is de afstand tussen de top en de bodem.
Orthocentrum van een driehoek
De drie hoogten van een driehoek komen in een punt samen. Dat punt wordt het middelpunt van de driehoek genoemd .
Concreet: In de tekening staan de hoogtes en het middelpunt van de driehoek.
Om het middelpunt van een driehoek te bepalen, bepalen we het snijpunt van de twee hoogtelijnen in die driehoek.
Let op: a) Als de driehoek een scherpe driehoek is, ligt het orthocentrum binnen de driehoek.
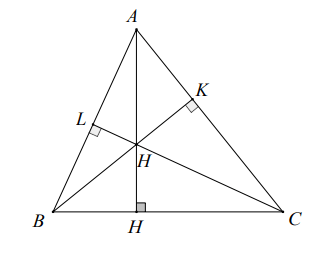
b) Als de driehoek een rechthoekige driehoek is, dan valt het orthocentrum samen met het punt .
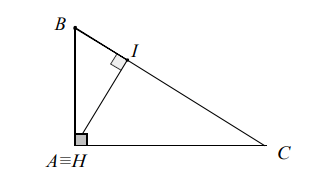
c) Als een driehoek stomp is, ligt het orthocentrum buiten de driehoek.
Eigenschap 1: In een gelijkzijdige driehoek zijn het zwaartepunt, het orthocentrum, een punt op gelijke afstand van de drie hoekpunten van de driehoek, een punt in de driehoek en op gelijke afstand van de drie zijden van de driehoek, vier samenvallende punten.
Eigenschap 2: Het orthocentrum snijdt de middelloodlijn van twee zijden in twee gelijke lengtesegmenten. Dit betekent dat het orthocentrum zich op gelijke afstand van de hoekpunten van de driehoek bevindt.
Eigenschap 3: Het orthocentrum is het middelpunt van de omgeschreven cirkel van een driehoek. Dit betekent dat als we een cirkel tekenen die door de drie hoekpunten van een driehoek gaat, het orthocentrum het middelpunt van die cirkel zal zijn.
Eigenschap 4: Het orthocentrum van een scherpe driehoek ligt binnen de driehoek, terwijl het orthocentrum van een stompe driehoek buiten de driehoek ligt.
Eigenschap 5: Het middelpunt van een rechthoekige driehoek valt samen met de top van de rechte hoek van die rechthoekige driehoek.
Eigenschap 6: Het orthocentrum is het enige punt in een driehoek. Als we lijnen trekken van het orthocentrum naar de hoekpunten van de driehoek, is de som van de lengtes van die lijnen het kleinst. Dit betekent dat het orthocentrum het dichtst bij de hoekpunten van de driehoek ligt dan enig ander punt.
Eigenschap 7: Het orthocentrum is tevens het middelpunt van de omgeschreven cirkel van de driehoek, dat wil zeggen de grootste cirkel die door de drie hoekpunten van de driehoek kan worden getrokken.
Bijvoorbeeld: Gegeven niet-kwadratisch. Noem het orthocentrum. Geef de hoogte van de driehoek aan. Geef daar het middelpunt van de driehoek aan.
Oplossingsgids
Illustratie
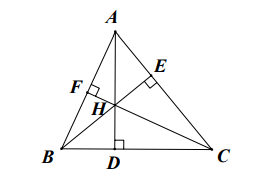
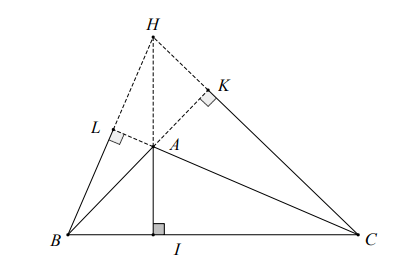
Laat de voeten van de loodlijnen getrokken uit ΔABC zijn.
Beschouw ΔHBC met:
AD is dus de hoogte van H naar BC.
bij F is BA dus de hoogte van B naar HC
bij E is CA dus de hoogte van C naar HB.
snijden elkaar in A, zodat A het orthocentrum is van ΔHCB.
Bijvoorbeeld: Gegeven een rechthoekige driehoek met hoogte . Laat het middenpunt van zijn, het middenpunt van is . Bepaal het middelpunt van de driehoek.
Oplossingsgids
Beschouw het deelprobleem als de driehoek en AC als middens heeft, dan zijn en .
Neem inderdaad op de tegenoverliggende straal van de straal een punt zodat
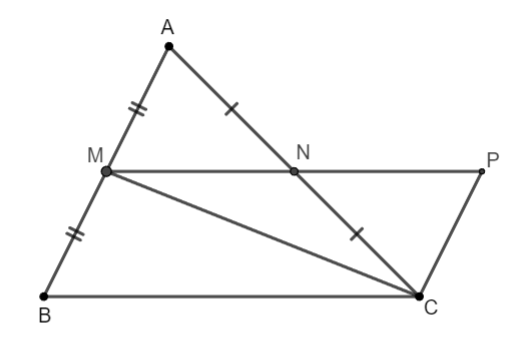
Beschouw driehoek AMN en driehoek CPN.
(tegenovergestelde)
, (twee zijden en twee overeenkomstige hoeken)
Twee hoeken staan in afwisselende posities, dus
=>(twee afwisselende binnenhoeken)
Beschouw driehoek BMC en driehoek PCM.
(cmt)
MC is een veelvoorkomende rand
, (overeenkomstige zijden en hoeken)
Twee hoeken staan in afwisselende posities, dus
We hebben weer
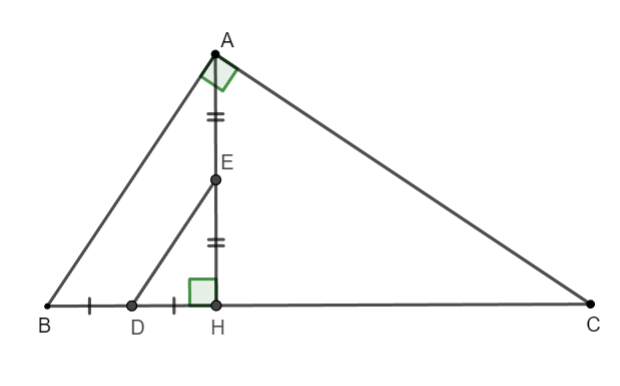
Beschouw driehoek HAB met:
(zoals hierboven bewezen)
Beschouw driehoek ADE.
aan de andere kant en
is de hoogte van driehoek ADE
C is het snijpunt van AC en DC
=> C is het orthocentrum van driehoek ADE
Bijvoorbeeld: Gegeven een schaal op A, snijdt de hoogte de mediaan op . Bewijzen en berekenen?
Instrueren
Illustratie
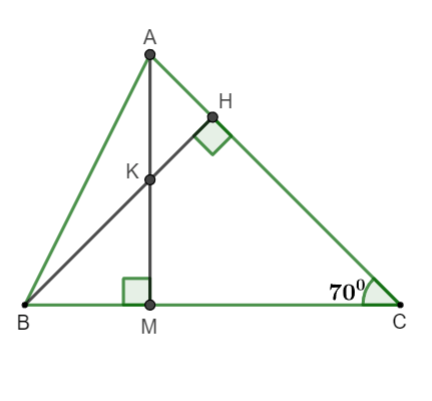
Omdat het saldo op A staat en AM de mediaan is
⇒ AM is ook de hoogte die overeenkomt met BC
Geldautomaat.
Aan de andere kant is K dus het orthocentrum.
K behoort dus tot de hoogte van C van ∆ABC.
Wij hebben:
In dit artikel leggen we je uit hoe je weer toegang krijgt tot je harde schijf als deze kapot is. Laten we het artikel volgen!
Op het eerste gezicht lijken AirPods op alle andere echt draadloze oordopjes. Maar dat veranderde allemaal toen een paar onbekende functies werden ontdekt.
Apple heeft iOS 26 geïntroduceerd: een grote update met een gloednieuw matglasontwerp, slimmere ervaringen en verbeteringen aan bekende apps.
Studenten hebben een specifiek type laptop nodig voor hun studie. Deze moet niet alleen krachtig genoeg zijn om goed te presteren in hun studierichting, maar ook compact en licht genoeg om de hele dag mee te nemen.
Het toevoegen van een printer aan Windows 10 is eenvoudig, hoewel het proces voor bekabelde apparaten anders is dan voor draadloze apparaten.
Zoals u weet, is RAM een zeer belangrijk hardwareonderdeel van een computer. Het fungeert als geheugen voor de verwerking van gegevens en is de factor die de snelheid van een laptop of pc bepaalt. In het onderstaande artikel laat WebTech360 u zien hoe u met behulp van software in Windows RAM-fouten kunt opsporen.
Smart-tv's hebben de wereld veroverd. Dankzij zoveel geweldige functies en internetverbinding heeft technologie de manier waarop we televisiekijken veranderd.
Koelkasten zijn vertrouwde apparaten in huishoudens. Koelkasten hebben meestal twee compartimenten. Het koelvak is ruim en heeft verlichting die automatisch aangaat wanneer de gebruiker het vak opent. Het vriesvak is smal en heeft geen verlichting.
Wi-Fi-netwerken worden niet alleen beïnvloed door routers, bandbreedte en interferentie, maar er zijn een aantal slimme manieren om uw netwerk te versterken.
Als u terug wilt naar de stabiele iOS 16 op uw telefoon, vindt u hier de basisgids voor het verwijderen van iOS 17 en downgraden van iOS 17 naar 16.
Yoghurt is een heerlijk voedingsmiddel. Is het goed om elke dag yoghurt te eten? Hoe verandert je lichaam als je elke dag yoghurt eet? Laten we het samen ontdekken!
In dit artikel worden de meest voedzame rijstsoorten besproken en hoe u de gezondheidsvoordelen van de rijst die u kiest, optimaal kunt benutten.
Een slaapschema en bedtijdroutine opstellen, uw wekker verzetten en uw dieet aanpassen zijn enkele maatregelen die u kunnen helpen om beter te slapen en 's ochtends op tijd wakker te worden.
Huren alstublieft! Landlord Sim is een simulatiespel voor mobiel op iOS en Android. Je speelt als verhuurder van een appartementencomplex en begint met het verhuren van een appartement. Je doel is om het interieur van je appartement te verbeteren en het gereed te maken voor huurders.
Ontvang de Roblox-gamecode voor Bathroom Tower Defense en wissel deze in voor geweldige beloningen. Ze helpen je bij het upgraden of ontgrendelen van torens met hogere schade.
