Formule voor het berekenen van de hoogte in regelmatige, gelijkbenige, gelijkzijdige en rechthoekige driehoeken

De hoogtelijn in een driehoek is een rechte lijn met belangrijke eigenschappen en hangt nauw samen met problemen uit de vlakke meetkunde. Dus wat is de hoogte en hoe bereken je de hoogte in een driehoek? Raadpleeg het onderstaande artikel voor het antwoord en de eenvoudigste formule om de hoogte van een driehoek te berekenen.

Inhoudsopgave

• Formule voor het berekenen van de hoogte in een driehoek
  • Bereken de hoogte in een regelmatige driehoek
  • Bereken de hoogte in een gelijkzijdige driehoek
  • Formule voor het berekenen van de hoogte in een rechthoekige driehoek
  • Formule voor het berekenen van de hoogte in een gelijkbenige driehoek
• Definitie van hoogte in een driehoek
• Eigenschappen van de drie hoogten van een driehoek

Formule voor het berekenen van de hoogte in een driehoek

Bereken de hoogte in een regelmatige driehoek

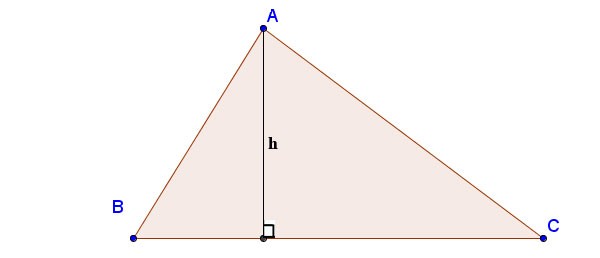
Hoe bereken je de hoogte van een driehoek met behulp van de formule van Heron:

Met a, b, c de lengtes van de zijden; ha is de hoogte getrokken van hoekpunt A naar zijde BC; p is de halve omtrek:

Bijvoorbeeld: 

Gegeven driehoek ABC, zijde AB = 4 cm, zijde BC = 7 cm, zijde AC = 5 cm. Bereken de hoogte AH van A die BC snijdt in H en bereken de oppervlakte van ABC.

Prijs:

Halve omtrek van de driehoek: P = (AB + BC + AC) : 2 = (4 + 7 + 5) : 2 = 8 (cm)

Hoogte   

=>

Beschouw driehoek ABC. We hebben:

Dus,

Bereken de hoogte in een gelijkzijdige driehoek

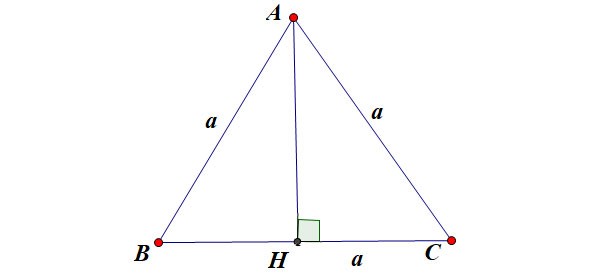
Veronderstel dat gelijkzijdige driehoek ABC zijde a heeft zoals weergegeven in de figuur:

Daarin:

• h is de hoogte van een gelijkzijdige driehoek
• a is de zijdelengte van een gelijkzijdige driehoek

Formule voor het berekenen van de hoogte in een rechthoekige driehoek

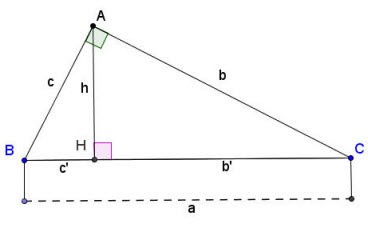
Veronderstel dat er een rechthoekige driehoek ABC is in A, zoals hierboven weergegeven:

Formule voor het berekenen van zijden en hoogtes in een rechthoekige driehoek:

1. a2 = b2 + c2

2. b2 = ab′ en c2 = ac′

3. ah = bc

4. h2 = b′.c'

5.

Daarin:

• a, b, c zijn de zijden van een rechthoekige driehoek zoals hierboven weergegeven;
• b' is de projectie van rand b op de hypotenusa;
• c' is de projectie van rand c op de hypotenusa;
• h is de hoogte van een rechthoekige driehoek, getekend vanaf het hoekpunt van rechte hoek A tot aan de hypotenusa BC.

Voorbeeld 1: Gegeven driehoek ABC met een rechte hoek in A, hoogte AH. Bereken BC, AC, AH met de kennis dat AB = 15 cm, HC = 16 cm.

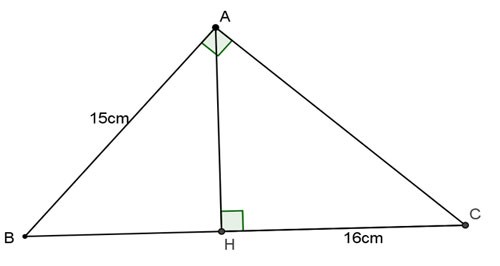
Prijs:

Als we de algebraïsche formule in rechthoekige driehoek ABC toepassen, krijgen we:

AC2 = CH.BC = 16.BC

Volgens de stelling van Pythagoras voor rechthoekige driehoek ABC met rechte hoek A geldt:

AB2 + AC2 = BC2

⇔ 152 + 16.BC = BC2

⇔ BC2 - 16.BC - 225 = 0

⇔ BC2 - 25.BC + 9.BC - 225 = 0

⇔ BC(BC - 25) + 9(BC - 25) = 0

⇔ (BC - 25)(BC + 9) = 0

⇔ BC = 25 of BC = -9 (elimineren)

⇒ AC2 = 16.BC = 16,25 = 400 ⇒ AC = 20 (cm)

Beschouw rechthoekige driehoek ABC met: AH.BC = AB.AC (meetkundige formule)

=> AH = AB.AC/BC = 15,20/25 = 12(cm)

Dus BC=25(cm); AC=20(cm); AH=12(cm)

Voorbeeld 2 :

Gegeven dat driehoek ABC een rechte hoek heeft in A, geldt: AB=24cm, AC=32cm. De middelloodlijn van BC snijdt AC en BC respectievelijk in D en E. Bereken DE.

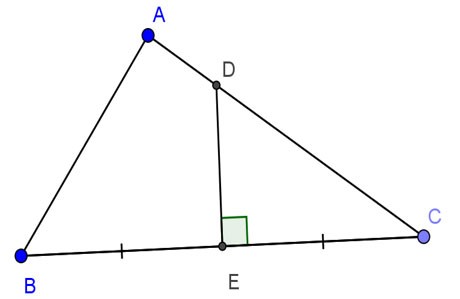
Prijs:

Beschouw driehoek ABC. We hebben:

BC2 = AB2 + AC2 (volgens de stelling van Pythagoras)

BC2 = 242 + 322

BC2 = 1600

BC = 40(cm)

EC = BC : 2 = 40 : 2 = 20 (cm)

Beschouw rechthoekige driehoek ACB en rechthoekige driehoek ECD met:

Er is ∠A = ∠E = 90o

∠C gemeenschappelijk

=> Driehoek ACB ∾ driehoek ECD (gg)

=> AC/EC = AB/ED

=> ED = AB.EC/AC = 15cm

Dus ED = 15cm

Formule voor het berekenen van de hoogte in een gelijkbenige driehoek

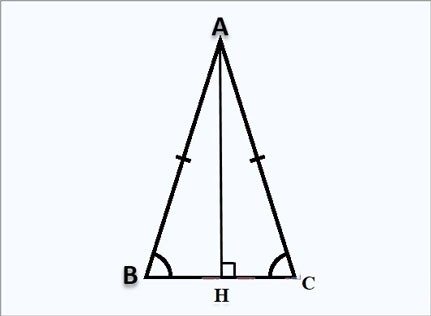
Stel dat je een gelijkbenige driehoek ABC hebt in A, en de hoogte AH staat loodrecht op H, zoals hierboven weergegeven:

Formule voor het berekenen van de hoogte AH:

Omdat driehoek ABC gelijkbenig is in A, is de hoogte AH ook de mediaan, dus:

⇒ HB=HC= ½BC

Als we de stelling van Pythagoras toepassen op de rechthoekige driehoek ABH, precies in punt H, dan krijgen we:

AH²+BH²=AB²

⇒AH²=AB²−BH²

Bijvoorbeeld : Gegeven Δ ABC is in evenwicht bij A met BC = 30 (cm), hoogte AH = 20 (cm). Bereken de hoogte die overeenkomt met de zijde van de gelijkbenige driehoek.

Oplossing: Beschouw Δ ABC als gelijkbenig in A met BC = 30(cm)

⇒ BH = CH = 15(cm).

Als we de stelling van Pythagoras toepassen, krijgen we:

Nu moeten we BK = ? berekenen

Wij hebben:

Anderzijds

Daarom hebben we ⇔

Definitie van hoogte in een driehoek

Een hoogtelijn in een driehoek is een loodrecht lijnstuk dat van een hoekpunt naar de tegenoverliggende zijde wordt getrokken. Deze tegenoverliggende zijde wordt de basis genoemd en komt overeen met de hoogte. De lengte van de hoogte is de afstand tussen de top en de bodem.

Eigenschappen van de drie hoogten van een driehoek

De drie hoogten van een driehoek lopen door hetzelfde punt. Dat punt wordt het middelpunt van de driehoek genoemd .

Om de hoogte van een driehoek te kunnen berekenen, hoeft u alleen maar de onbekende componenten in de bovenstaande formules mee te rekenen.

• Waar ligt de focus? Formule voor het berekenen van het zwaartepunt van een driehoek